どうも、丸田です。
数学のおける、永遠のテーマでもある「無限」。
その響きだけで、なんだか好奇心くすぐられるような気がしますよねぇ。
無限は、紀元前からすでに考えられていた神秘的な概念ですが、その難解さから、数多くの天才たちを悩ませてきた厄介なモノでもあります。
そんな長年の無限に対する、最終結論を導き出したのが、ドイツの数学者ゲオルク・カントールでした。
彼が発見した無限のさらに奥深くには、人類の五感をはるかに超えた摩訶不思議な世界が広がっているのです。
ということで今回は無限の果てに広がっていた世界がどのようなものだったのか?について、わかりやすくご紹介していきます。
ぜひ最後まで楽しんでください。
※今回の記事における、無限とは「無限の大きさ」にフォーカスして解説しております。
無限に潜む、さまざまなパラドックス
そもそも無限とは何なのでしょうか?
言葉の定義は以下となります。
無限(むげん、infinity、∞)とは、限りの無いことである。
「限界を持たない」というだけの単純に理解できそうな概念である一方で、有限な世界しか知りえないと思われる人間にとって、無限というものが一体どういうことであるのかを厳密に理解することは非常に難しい問題を含んでいる。このことから、しばしば哲学、数学、論理学や自然科学などの一部の分野において考察の対象として無限という概念が取り上げられ、そして深い考察が得られている。
ザックリ言えば、「限りがない」という認識でOKです。
この限りがない概念が故に、さまざまな哲学的問題が浮かび上がってくるのです。
アキレスと亀
「アキレスと亀」とは、紀元前500年頃に活躍したギリシャの哲学者ゼノンが提唱したパラドックスのひとつです。
俊足のアキレスが、亀に少し先にスタートさせて競争するとします。
アキレスが亀のいた場所に到達する頃には、亀は少し前に進んでおり、さらにアキレスが進んだ頃には、また亀も少し前に進んでいることになります。
これを繰り返すとアキレスは永遠に亀に追いつけないことになります。
現実的には、当然アキレスはすぐに亀を追い抜いてしまいますが、論理の世界だと、この誤りをなかなか証明できずにいたのですね。
これは「無限に分割された距離」が問題の核心ですが、現代数学ではそれが有限に収束するため、アキレスは実際には追い抜けると説明されています。
無限の猿定理
仮に、時間も体力も無限に持っているチンパンジーが存在するとしましょう。
そして、チンパンジーにタイピングをしてもらいます。
チンパンジーはキーボードをランダムにタイピングするでしょうが、無限にタイピングでき、無限に時間がある(寿命がない)と考えるなら、チンパンジーがランダムに打った文字列の中には小説「ハムレット」が書かれるという話です。
これを「無限の猿定理」と言います。
※ちなみに、おおよそ10の300万乗年という果てしない時間をかければ理論上は可能とされているそうです。
円周率のはどんな数字の羅列も含まれる?

円周率は(π)は3.141592…と小数点以下無限に続く数です。
この永遠に続く数字は限りなくランダム(法則性はない)だと言われています。
無限に続くということは、もちろん「12,3,4,5,6,7,8,9」みたいな並びも存在するということです。
そしてその中に、あなたの電話番号が含まれているのです。
このような無限に関するさまざまな考え方があるのです。
まさに無限の可能性を含んだ無限という概念を扱うことに、多くの哲学者・数学者たちは悩んでいたのです。
誰もが嫌った無限の世界を冒険したチャレンジャー現る!
果てしなく無限に広がった数字を扱うことは、いつしか神や畏怖の対象として恐れられ、多くの学者が避け始めました。
かのガリレオですらも、無限について考えることをやめたと言います。
ここで、無限を嫌った科学者たちの声をご紹介しましょう笑
無限は有限と同じに扱うことはできない
素数の個数はいかなる定められた素数の個数よりも多い(※素数は無限に存在するんだけど、無限という言葉は使いたくない)
無限の概念をただ神のみ保留する
わたしは無限量を1つの完結した量として用いることに反対です。そのようなものの使用は数学ではけっして許されません。
という感じで、無限=神、あるいは人間が扱うべきではない概念として考え、数学には取り入れようとしなかったのです。
そんな無限を前に天才たちがざわつく中、「オレ行きます!」と勢いよく名乗り出た数学者がいました。
それがドイツの数学者、ゲオルク・カントール(1845〜1918)でした。
ゲオルク・カントールはもともと実数や関数の研究を行っていたのですが、その過程で無限が絡む問題に取り組むようになりました。
そして、ついに彼は禁断の疑問を抱いたのです。
「無限にも大きい無限、小さい無限などは存在するのだろうか?」
この問いがきっかけに、彼の人生賭けた無限の探究が始まったのです。
抽象度高すぎる無限という概念。
そんな概念を扱いやすくした画期的な数学の発明をカントールは行いました。
それが「集合論」です。
集合論は、現代数学の基礎として必要不可欠の概念なのですが、カンタンに説明すれば、この集合論は、無限という概念を扱うための入れ物としての役割を果たします。
そして、その無限を含んだ入れ物がどのように構成され、分類されるかを明らかにすることで無限の解明を試みたのでした。
彼は周囲の声や反論、また自身ですらも信じられないような論証を目の当たりにしながらも、なんとか無限の解明を突き進め、そしてエゲツナイ最終結論を導いてしまったのでした。
無限を扱うための言葉
ではここからは、無限の果てにあった世界をご紹介します。
その前に、まずは数学における「無限」の定義や必要な用語などを簡単にご紹介します。
数の集合
まずは数における集合を定めます。
と言っても難しく考える必要はありません。数字を分類するだけです。
以下のように数字を分類した、無限集合を考えます。
- N:自然数(マイナス、0を除く1,2,3…の数字)
- Ne:偶数の自然数
- No:奇数の自然数
- Z:整数(分数・少数点を除く数、-2,-1,0,1,2,3…など)
- Q:有理数(主に分数 2/3, 1/2, 5/2 など。※4/2=2など割れる数も有理数)
- C:複素数(虚数を含む数)
- R:実数(マイナス、0、分数、円周率など。虚数を除くすべての数)
これらの数の集まりは、無限の個数を持つ無限集合たちです。
ここで、クイズです。
これらの無限集合でどれが大きく、どれが小さいか?わかりますか?
答え
1(自然数)=2(偶数の自然数)=3(奇数の自然数)=4(整数)=5(有理数)<6(実数)=7(複素数)
となります。
なんだか不思議ではありませんか?
だって、偶数の数字たちと偶数と奇数混ぜた数字たちが、無限という観点からすれば同じ大きさだと言っているのですから。
ちなみに、自然数、偶数、奇数、整数、有理数を可算集合といいます。
無限の定義・測り方
では、これから無限の定義と測り方をご紹介します。
まず数学上における無限の定義です。
Xは無限集合であるとは?X≠Φかつ∀x∈N, X≠{1,2,3,4,…n}
まぁ意味不明だとは思いますが笑
つまり、無限というのは、どんな有限な値を選んでも、それを超えていくということです。
イメージは、1万という数字を思い浮かべても、それより大きい数字は思い浮かぶし、6000京!という数字を思い浮かべても、それよりも大きな数字が思い浮かぶ(例えば、6001京みたいな)ということです。
これが無限の定義です。
そして、この無限同士の大きさを比較するにはどうすれば良いのか?
専門的に言えば、全単射が存在するかどうかというややこしい話になりますので、きのこの山とたけのこの里で例えます!笑
きのこの山とたけのこの里、それぞれの箱があるとします。
それぞれの箱の中のお菓子の数、どちらが多いかをこれから数えたいです。
とは言え、数学者ですから、厳密に数えたい!絶対に目視で数えるのではなく、確実に完璧に数えたい!
じゃあどうするか?というと、ペアを作って数える方法を取るのです。
つまり、きのこの山の箱から、1つお菓子を取る。次にたけのこの里の箱から、1つお菓子を取る。
それらを1対1でペアとして数えます。
それを続けていき、もしきのこの山が余れば、きのこの山の方が多いとわかるし、たけのこの里が余れば、たけのこの里の方が多いとわかりますよね。
そして、もしペアを作って、お互いの箱の中が空になれば、個数が同じだったということもわかります。
この原理を無限集合にも応用することを考えました。
集合の個数を厳密には、「濃度」と言います。
そして、同じ個数だった場合は、全単射が存在すると表現します。
このような無限の定義、そして無限の測り方を行うことで、カントールは無限の大小を比較することにしていったのです。
上記のような定義に沿って、無限を測った結果
- N:自然数(マイナス、0を除く1,2,3…の数字)
- Ne:偶数の自然数
- No:奇数の自然数
- Z:整数(分数・少数点を除く数、-2,-1,0,1,2,3…など)
- Q:有理数(主に分数 2/3, 1/2, 5/2 など。※4/2=2など割れる数も有理数)
- C:複素数(虚数を含む数)
- R:実数(マイナス、0、分数、円周率など。虚数を除くすべての数)
これらの無限集合の大小は、
1(自然数)=2(偶数の自然数)=3(奇数の自然数)=4(整数)=5(有理数)<6(実数)=7(複素数)
となるわけです。
無限の果てにある世界
ではここから、実際に無限の大小を測っていきましょう。
まず一般的に我々が扱う数字、自然数とその中の偶数だけの集合が同じであることは以下のような数え方で証明できます。
自然数と自然数の偶数の集合の濃度が等しい
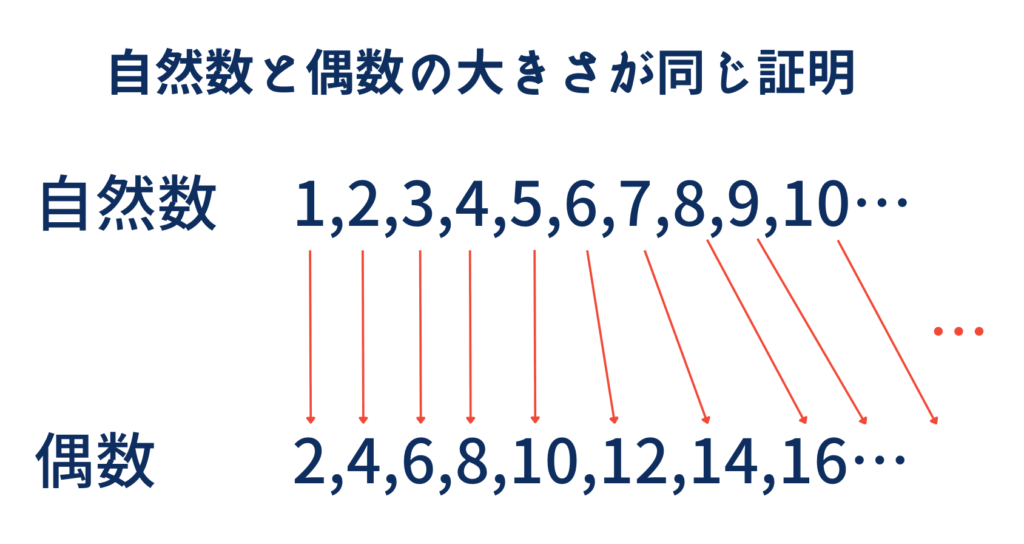
自然数nに対して、2nを対応させれば、偶数全体と自然数全体が一対一対応(ペア)にできます。
お互いの集合は無限ですので、どこまでもペアを作り続けることができます。
よって自然数と自然数の偶数の集合の濃度が等しいと言えるのです。
自然数と自然数の奇数の集合の濃度が等しい

自然数nに対して、2n+1を対応させれば、奇数全体と自然数全体が一対一対応(ペア)にできます。
お互いの集合は無限ですので、どこまでもペアを作り続けることができます。
よって自然数と自然数の偶数の集合の濃度が等しいと言えるのです。
自然数と整数の集合の濃度が等しい

自然数Nに対し、整数は正と負の数を含むため、一見すると自然数より「多い」ように見えます。
しかし、数学的にはどちらも濃度は等しいのです。
実際に、自然数に対してジグザグに整数を対応させる関数(例:f(n)=(−1)n⌊n/2⌋f(n) = (-1)^n \lfloor n/2 \rfloorf(n)=(−1)n⌊n/2⌋)を作ることで、全単射が構成できます。無限集合の世界では、直感に反して「より多く見えるもの」と「少なく見えるもの」が、数学的には同じ大きさになるのです。
自然数と有理数の集合の濃度が等しい


すべての分数を順番にリストアップして、自然数と1対1で結びつける工夫ができます。無限の世界では、「数えられる」ということが「同じ大きさ」を意味するのです。
さらに、他にもさまざまな信じられない定理が見つかりました。
- 無限集合Aとして、そのAの内部に入った無限集合Bの濃度は等しい
- 整数と整数の2乗の無限集合の濃度は等しい
無限より大きな無限の発見
さらにここからトンデモない理論が始まります。
それは今まで考えてきた無限よりも、さらに大きな無限が見つかっていくのです。
自然数より実数の集合の濃度が大きい(対角線論法)
まず結論から言いますと、今まで考えてきた無限は、実数という集合の一部に収まっています。
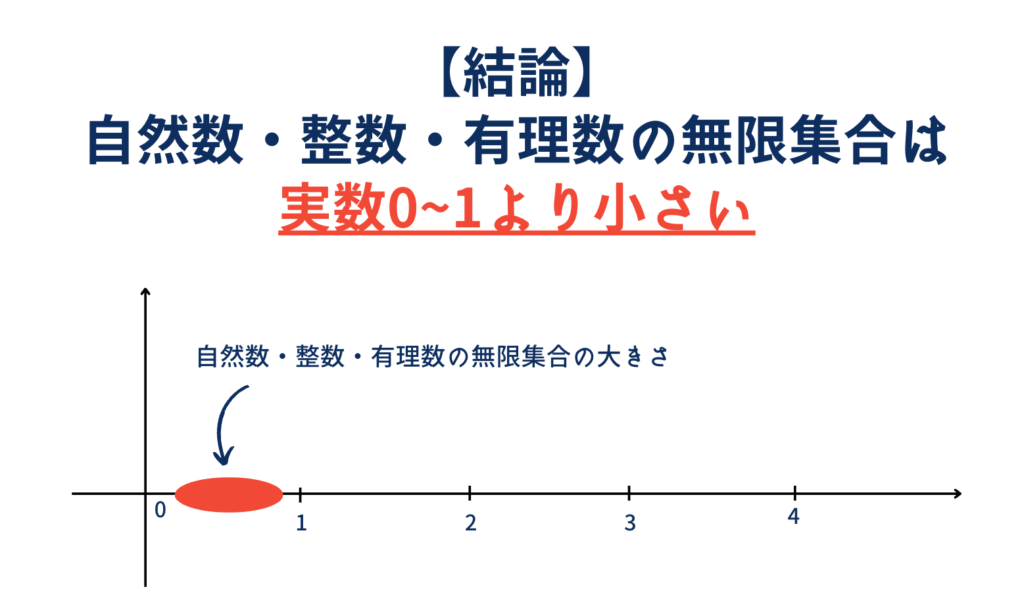
これは少し複雑ですが、カントールの対角線論法という手法で証明されます。
まず考える範囲は、実数の0<x<1の範囲でOKです。
自然数は1、2、3…と順番に数えられる数。実数は、小数や分数もふくめた“数のすべて”を含む集合です。では、実数のほうが「多い」とはどういう意味でしょう?
カントールは、実数はどんなに頑張っても順番に並べきれないことを証明しました。
その方法が「対角線論法」。
すべての実数を小数で書いてリストにしても、そのリストにのっていない新しい実数をつくる方法があるのです。
つまり、自然数では数えきれないほど、実数は“ぎっしり無限”にあるということ。無限にも“濃さ”の違いがある——そんな驚きの事実が、数学では明らかになっているのです。
実数と複素数の集合の濃度が等しい
実数とは、整数や小数、無理数など“数直線のすべて”をふくむ数。
複素数はそれに「i(アイ)」という新しい数を加えたもの。たとえば「3 + 2i」のように、実数と i を組み合わせてできています。
一見すると、複素数の方が“数の種類が多い”ように思えますよね? でも実は、数学的には実数も複素数も同じだけ無限にあるとされています。
なぜなら、複素数は「実数どうしのペア」で表せるからです。たとえば「3 + 2i」は、実数のペア (3, 2) と同じ。
つまり、数の直線(実数)と、数の平面(複素数)には、同じ“濃さ”の無限があるのです。
カントールが命をかけて、無限にも大小が存在するということを発見したのでした。
無限の果てにあるもの
カントールの主張はこれだけでは終わりません。
これら無限を「超限数」と呼ぶことにしたのです。
ちなみに、カントールは神の領域にある完成された無限、言葉で表現できない無限は「絶対無限」と考えています。
さらには、自然数の集合を\(\aleph_{0}\)(アレフゼロ)、そして実数の集合を\(\aleph\)(アレフ)と定めたのです。
これらの無限にも、数を構築する際の原理を取り入れることによって、
\(\aleph_{0}\, \aleph_{1}\, \aleph_{2}\, \aleph_{3}\, \aleph_{4}\, \aleph_{5}\)…として定めたのです。
そして、以下のような式を導き出しました。

これは何か1つの無限が存在するなら、それより1つ上の無限を作り出せることを意味しています。
これを一般化すると、以下のように書き出されます。
これは、数学者ハウスドルフが一般化しました。
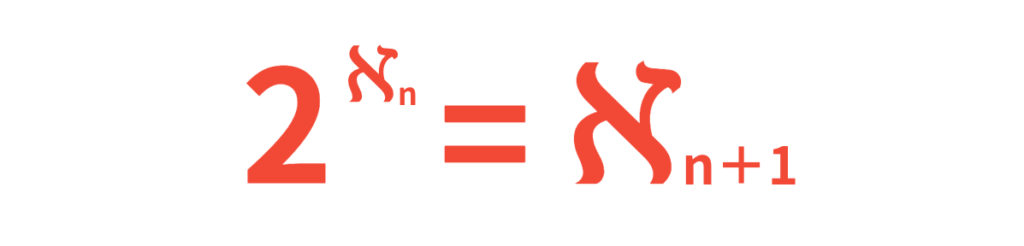
つまり無限の大小に関しての最終結論というのは、無限にも“大きさ”の違いがあるかもしれないという驚くべき事実だったのです。
「連続体仮説」
残念ながら、カントールはこの無限の主張を解決できずまま、その生涯を終えました。
のちにさまざまな数学者たちがこの問いに挑戦しました。
そして、ついに1940年に、哲学者クルト・ゲーデルの主張、
そして1963年にポール・コーエンの二人の主張によって、この連続体仮説は現在の集合論では解決すること自体が不可能であるということが証明されたのでした。
まとめ
今回は、無限の果てに広がる世界をについて解説しました。
数千年にわたって誰もが恐れた無限がどのように解明されていったのか?
そのプロセスはとても興味深いと同時に、なんともモヤモヤするような感覚も残っているのではないでしょうか?
結局、最後は証明すらできないという結論に至ったことから、とても生々しい論理の限界を感じざるを得ません。
それは無限という概念が、人類が開けてはならないパンドラの箱だったのか?それとも人類の知性がさらに発展する余地が残っているのか?
どう感じるかはアナタ次第です!











