どうも丸田です。
フェルマーの最終定理がどのように解決されたのか？を解説していきます。
とはいえ、専門的に解説するのは難しいため、なるべく噛み砕いて、少し厳密性などは取り除いた形となることをご了承ください。
どちらかといえば、歴史的な流れをメインに紹介していきたいと思います。
今回は、1700~1800年代の数学者たちの奮闘の歴史をご紹介します。
フェルマーの最終定理にどのようなアプローチをしたのか？
まずフェルマーの最終定理とはこのような問題です。
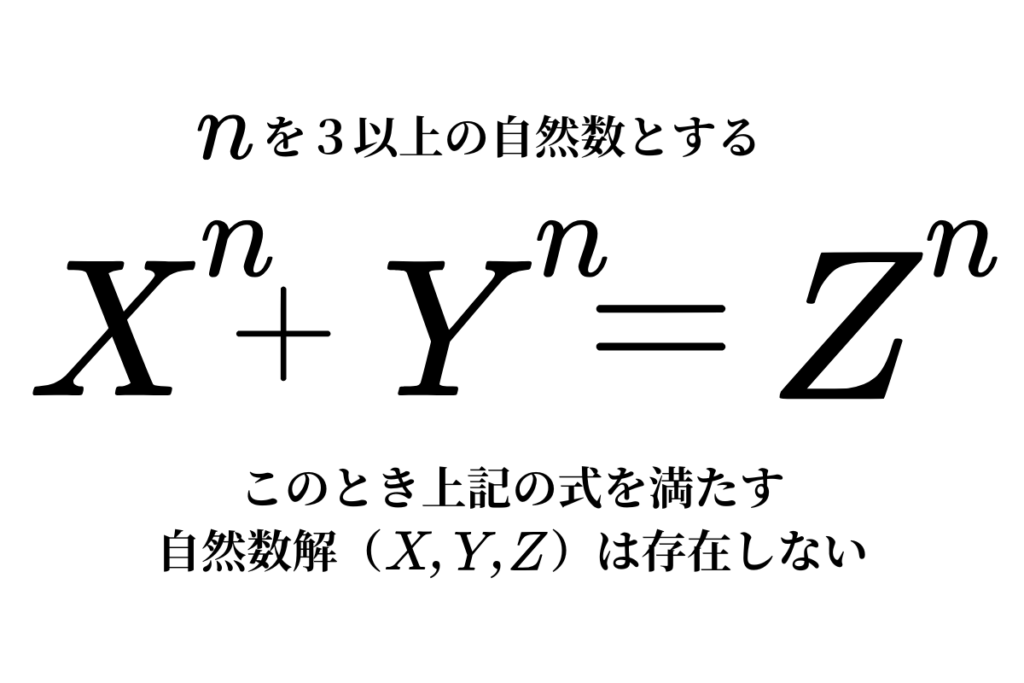
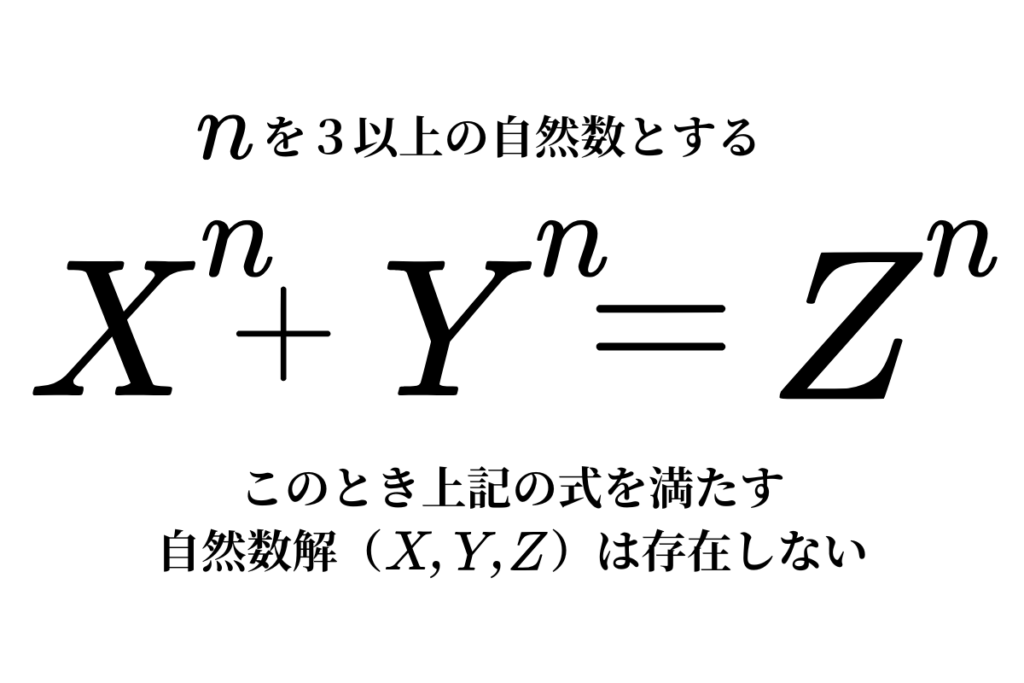
この存在しないことを証明しなければならないというのが、気が遠くなるほどの難しさを醸し出していますねぇ。
ちなみに、この問題は数学史上最も難問と言われており、なんと360年間解決されませんでした。
それゆえ、別名「悪魔の問題」などとも呼ばれており、数多の数学者が立ち向かっては返り討ちになりました。
そして天才数学者たちが、様々な数学理論を駆使して少しずつダメージを与えていき、最後の最後は、光の勇者がフェルマーの最終定理をぶちのめす！
まさに世代を超えて数学者たちが団結して解決した、激アツの物語なんですね〜！
RPGでイメージするなら、勇者一行が命をかけながら、敵にダメージを与えていき、最終的にみんなの力を借りて勇者がとどめをさす！
くぅ！シビれるッ…！
いかんいかん！
熱くなりすぎてダラダラしゃべってしまった！笑
前置きが長くなりましたが、本題に入ります。
史上最強の難問とされるフェルマーの最終定理を、天才たちはどのようにアプローチしていったのか？
この難問にはじめて大きく切り込んだのが、オイラーという数学者でした。
オイラーは1700年代に大活躍したスイスの数学者で、数学に没頭しすぎて両目が見えなくなってしまいました。にも関わらず、書いた論文数世界１の実績を持っており、心臓が止まる10分前ぐらいまで計算し続けていたと言われています。
彼が両目を失明した際に放った言葉は「おかげで気が散らなくなった。前より数学の研究に打ち込める」という、まさに数学モンスター。
おそらく人間じゃありません笑
彼はフェルマーの最終定理が1670年に、世に公表されてから、およそ100年後にようやく解決に一歩近づけた数学者となったのです。
オイラーは考えました。
「このnの部分を具体的にすることから始めたらよくね？」
つまりは、
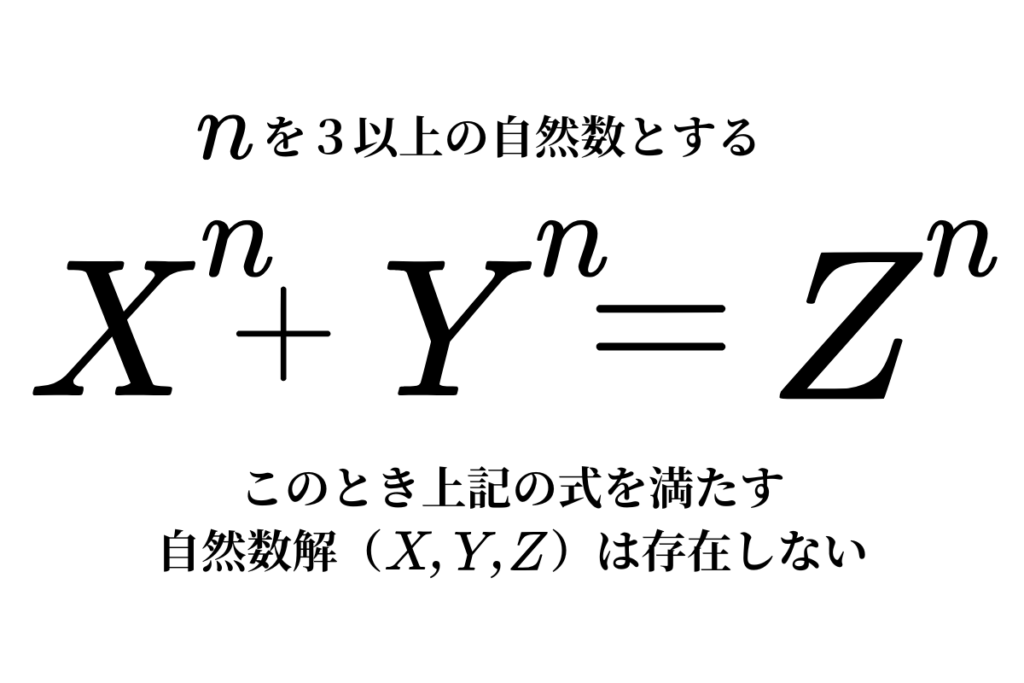
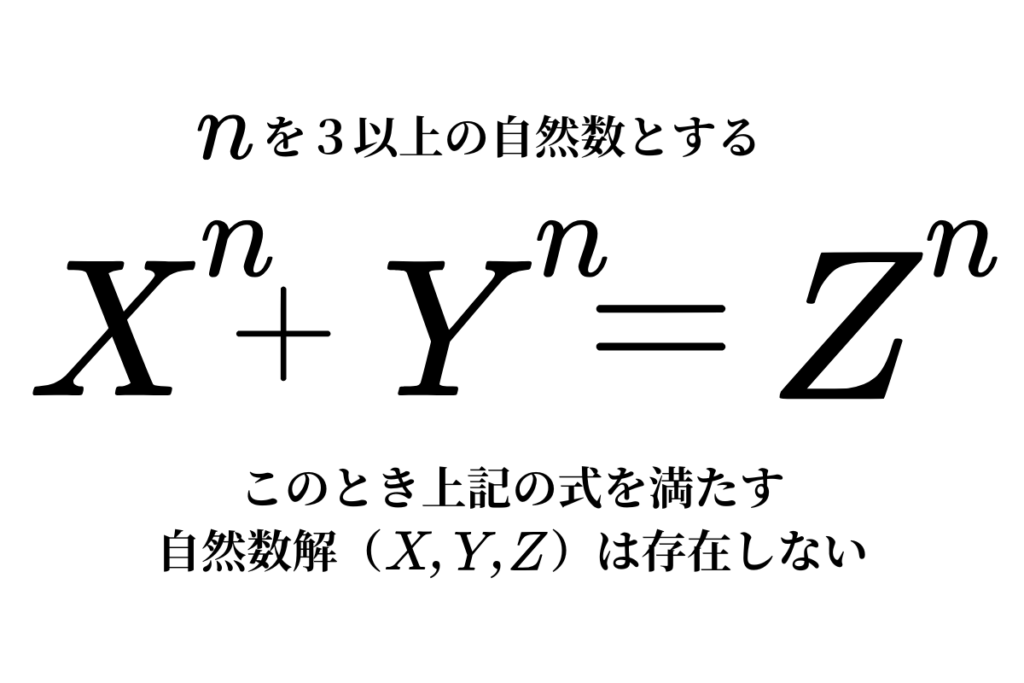
このnの値は、「3,4,5,6,7,8,9,10,11,12…」と無限に続くわけですが、まずは１つ具体的に値を入れてみるという発想でした。
さすがはオイラー！
このような取っ付きづらい問題は具体的にしてみるのがコツです。
ということで、フェルマーの最終定理のnに具体的な数字を入れてみるというアプローチが始まりました。
さらにオイラーは、過去のフェルマーの残した定理から、フェルマーの最終定理の解決に活用できそうな定理を調べました。
そして、とうとう手がかりを見つけました。
なんとフェルマーが本の余白に乱雑にメモ書きした定理の中に、さりげなくn=4の場合の証明を残していたのでした。
n=4の時 フェルマー
n=4の場合は、フェルマー自身が証明していました。
つまりは。
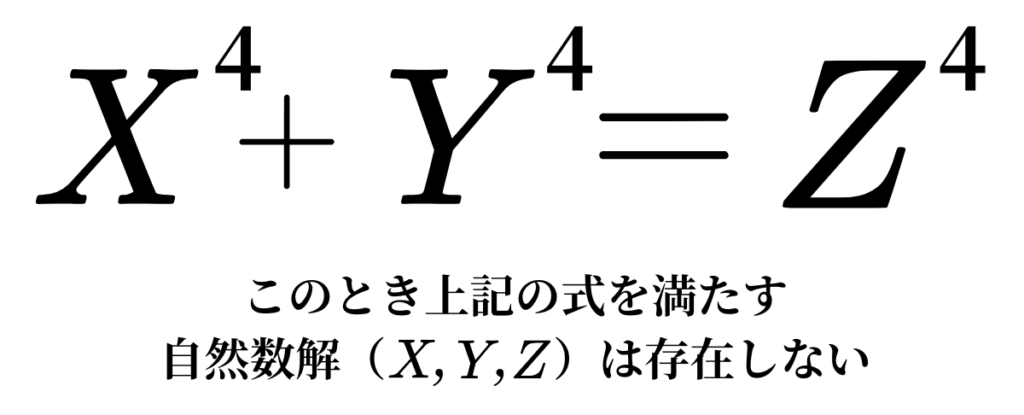
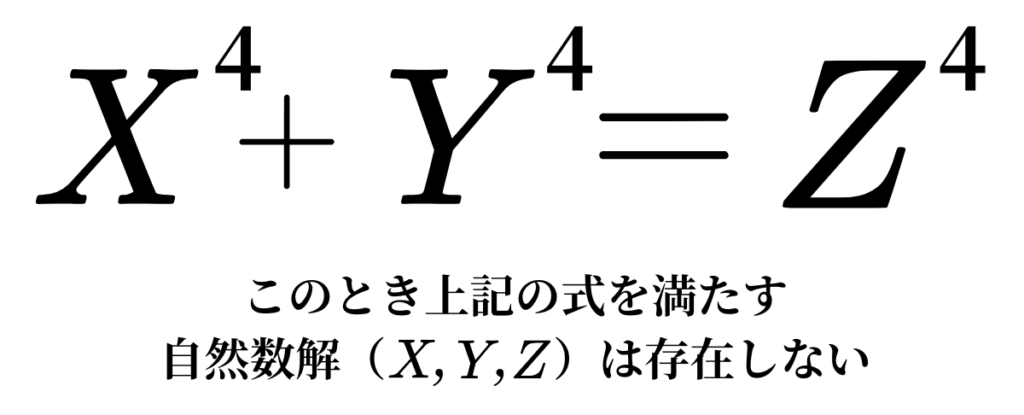
これを証明していたわけですね。
ではどのように証明したのか？フェルマーには必殺技がありました。
それが【無限降下法】という手法です。
この無限降下法とは一体なんなのか？
ザックリご紹介します。
無限降下法とは
無限降下法とは、\(x^{4}+y^{4}=z^{4}\)を満たす\(自然数(x,y,z)\)が存在すると仮定して、いろいろ計算した結果、この\(自然数の組み(x,y,z)\)が【いくらでも小さく】できる。しかし、\((x,y,z)\)は自然数のため、最小値が1。よって【いくらでも小さくできる】ことと、最小値が1であることが矛盾するため、最初の\(x^{4}+y^{4}=z^{4}\)を満たす\(自然数(x,y,z)\)が存在すると仮定が間違っていた。よって\(x^{4}+y^{4}=z^{4}\)を満たす\(自然数(x,y,z)\)は存在しない。
という証明です。
より詳しく解説していきます。
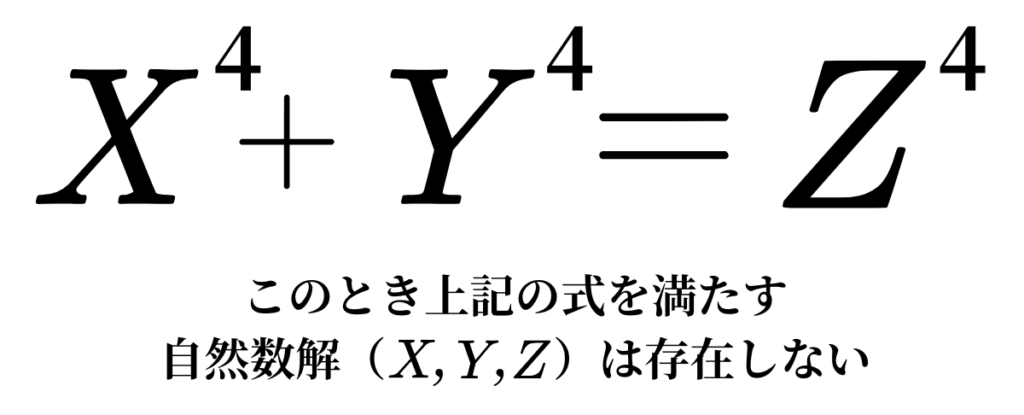
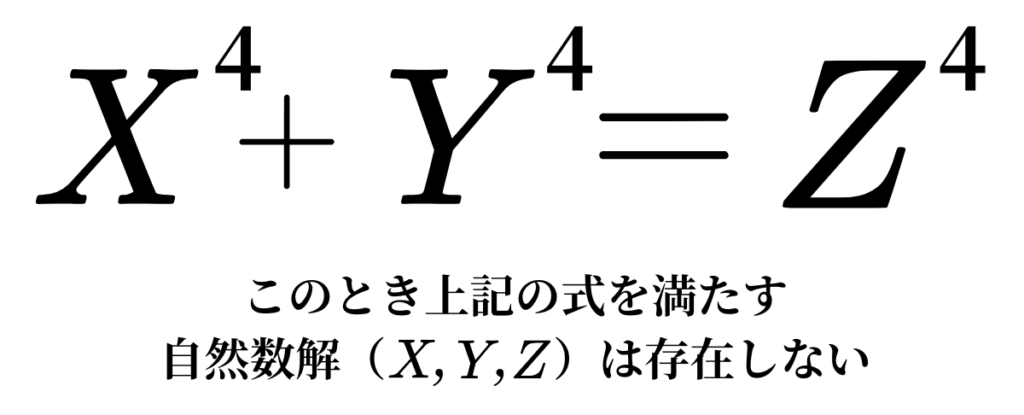
直接的に証明するのが難しい問題は、その主張を否定して考えることで突破口が見えてきます。
つまり、この方程式を満たす自然数の解\((X,Y,Z)\)が存在すると仮定して、論理展開した結果、何かしら矛盾が生じた場合、この方程式を満たす自然数の解\((X,Y,Z)\)は存在しないと結論づけることができます。
※このような、ある主張を証明する時、主張を否定して矛盾を導いて証明する方法を「背理法」と言います。
背理法とは、ある主張Aが正しいことを証明するのに、Ａが正しくないという前提で論理を展開し、矛盾が生じさせることで間接的にAが正しいと主張する証明法です。
実際に計算していきます。
ここはややこしいので軽く省略します。
ただ、ここである不思議な現象が起こります。
それはいくらでも小さな自然数の解\((X,Y,Z)\)が作れてしまうということです。
何ということでしょう！どこまでも無限に小さくなり続ける\((X,Y,Z)\)なんて！
しかし、そもそも自然数には最小値１が存在します。
自然数は１からスタートして2,3,4,5…と増えていく数字です。
逆を言えば、自然数は１が最小なんですね。
ここで先ほどの、どこまでも無限に小さくなる自然数が存在する一方で、そもそも自然数という概念には1という最小値が存在し、１より小さくなることはないという事実に矛盾が生じます。
よって、”この方程式を満たす自然数の解が存在するという仮定”自体がオカシイことになります。
よって間違っていたので、この方程式を満たす自然数の解は存在しない。という結論に至りました。
こうしてフェルマーは自身のフェルマーの最終定理のn=4の場合のみの証明を行っていました。
n=3の時 オイラー
とまぁ、そんな数学者オイラーがフェルマーの最終定理において、n=3の場合を証明しました。
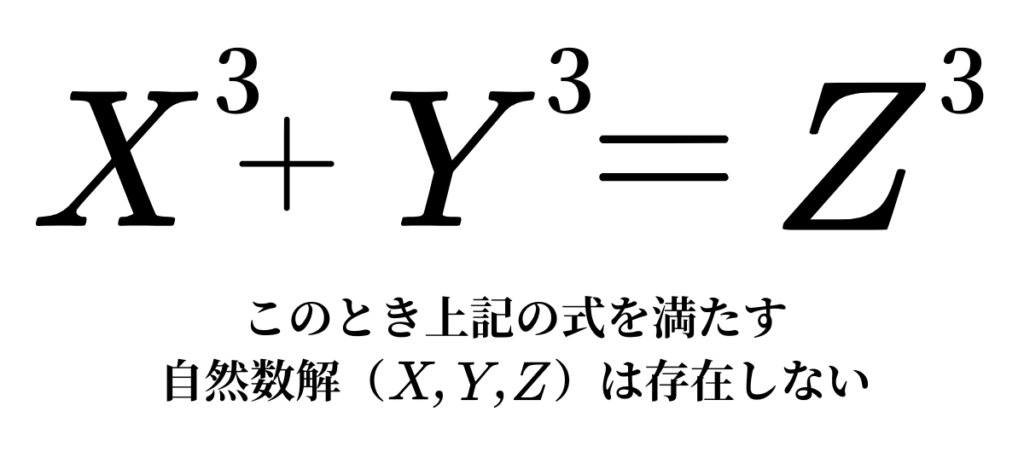
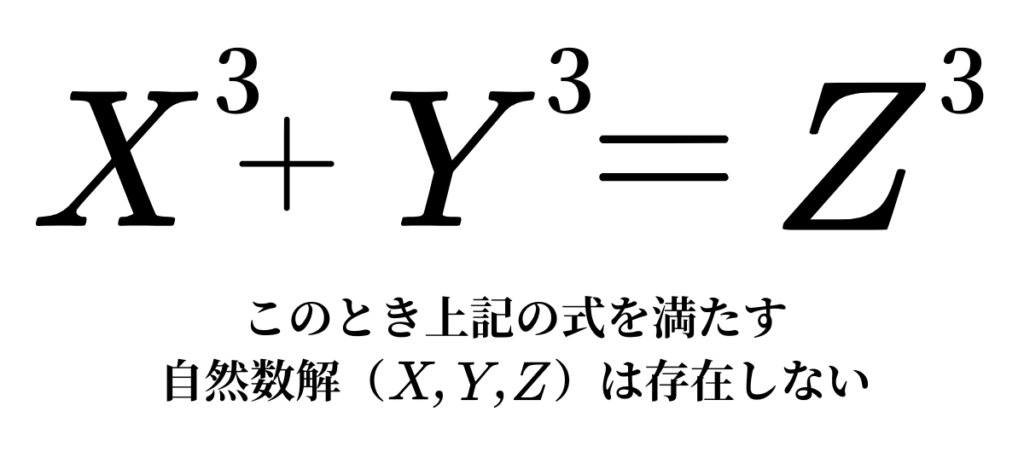
オイラーは、フェルマーのn=4の証明に使われた「無限降下法」を用いました。
しかし、ここで壁にぶち当たります。
なんとn=3の場合、無限降下法だけでは不十分だったのです。
困ったオイラー。そこで奥の手を使うのでした。
それが「虚数」という概念。
「虚数って存在するのか？」と質問される回数No.１を誇る、まさに数学界におけるMr.都市伝説である虚数。
虚数とは、簡単に言えば、数字を2乗するとマイナスになるという性質の数字です。
普通、数字は２乗すれば必ずプラスになります。それがマイナスになるという摩訶不思議。
もっと言えば、マイナス×マイナス＝マイナスになるというわけです。
中学で学んだ「マイナス×マイナスはプラス」とは一体なんだったんだ？と嘆きたくなるほど数学理論を根底から覆すのが虚数という概念なのです。
当時は虚数は怪しいと異端扱いされていました。
今でこそ、数学では虚数概念を当たり前のように扱いますが、数学者が虚数を用いることは、当時は禁忌、タブーとされていた見方もあり、1500年代に活躍したイタリアの数学者カルダノは「虚数をただ記号として取り入れよ。たとえ苦痛だとしても」という虚数に対しての苦悩な心境を吐露しています。
こうして、タブーとされていたオイラーはフェルマーが残した「無限降下法」と、虚数の概念を用いてフェルマーの最終定理、n=3の場合を証明したのでした。
ちなみに、当時は怪しいと異端扱いされていた虚数ですが、オイラーは虚数を表す「i」を提案し、のちの数学者ガウスは虚数をグラフ化に成功したことで、虚数は認められていきました。
ビジュアルが大事なんだなと考えさせられる話ですね〜。
しかしオイラーは気にせず虚数を使いました。
こうして、「無限降下法」と、切り札「虚数」を用いてフェルマーの最終定理のn=3の場合を証明したのでした。
ちなみに、当時は怪しいと異端扱いされていた虚数ですが、オイラーは虚数を表す「i」を提案し、のちの数学者ガウスは虚数をグラフ化に成功したことで、虚数は認められていきました。
ビジュアルが大事なんだなと考えさせられる話ですね〜。
n=3とn=4の場合が証明されたことで、フェルマーの最終定理の今後の展望は一気に切り開かれたのでした。
一気に詰める！
実は、n=4の場合に解が存在しないと言えるならば、nの値がn=8,12,16…、nの値が4の倍数のときも実は解が存在しないと言えるのです。
そして、4の倍数は2の倍数でもあるので、2の倍数、すなわち偶数においても解が存在しないことが言えます。
この段階で、すでにnの値が偶数の場合は全て解が存在せず、残すは奇数の場合に絞られました。
さらに、オイラーはn=3というとてもグッジョブな証明を果たしたのです。
というのも先ほどの理論と同様にn=3で証明されているのであれば、n=6,9,12,15,18…と３の倍数でも解が存在しないと言えるのです。
ここまでを整理すると、
nが自然数という条件において、
- nが偶数の場合は証明済み
- nが3の倍数の場合は証明済み
となりました。
残る証明すべきnの候補は、n=5,7,11,13,15,17,19,23,25,29…
絞られました。
さらに、ここでとある数学者が斬新な理論を提唱しました。
その数学者がソフィー・ジェルマンです。
n=5,7を証明完了！
ソフィージェルマンは新しい着眼点で理論を開拓しました。
それは「素数に注目すれば良い」ということです。
ここでなぜいきなり素数なのか？という話ですが、nの候補はこのようになりました。
n=5,7,11,13,15,17,19,23,25,29,31,35,37,39,41,43,47,49,53…
そのうち素数は以下の通り、
n=5,7,11,13,15,17,19,23,25,29,31,35,37,39,41,43,47,49,53…
つまり、残りの候補はほぼ素数なんですね。途中5の倍数と7の倍数が混じりますが、これは素数であるnが5と7の場合の証明できれば候補から消えます。
つまり、素数を攻略すればほぼ王手！というぐらいに証明完了までの距離を詰めることができるのです。
この事実に注目したソフィージェルマンは素数攻略へ踏み切ったのです。
そして生み出した理論がこれなんですね。
ソフィージェルマン素数という、素数を判定する方法です。
2p+1が素数となるような素数pをソフィー・ジェルマン素数という。
※2p+1が素数の場合、2p+1を「安全素数」という
さらに、ソフィージェルマンは以下のことを証明したのでした。
これによって、
この方法を確立したことで、フェルマーの最終定理へのアプローチの手数が増えたんですね。
この理論に注目したのが、ルジャンドルとディリクレという2人の数学者でした。
彼らは1825年にソフィージェルマンの理論を持ちいて、共同研究を行なった末n=5の場合を証明したのでした。
さらに14年後の、1839年に数学者ガブリエル・ラメがn=7の場合を証明したのでした。
厳密には、n=14の場合ですが、n=14を証明できれば、n=7も同様に証明できたことになります。
こうしてとうとう、nが3以上の自然数という果てしないnの候補は、nが3以上の素数の時、という範囲がギュッと絞られていったのでした。
とはいえ、フェルマーの最終定理への追及の旅はここで断念せざるを得なくなってしまいました。
なぜなら、この素数という概念自体が、人類が2000年近く考え尽くして、未だ糸口を見出せていない、数学史上最大のミステリーだからです。
素数の壁。そして終焉。
よっしゃ！nが3以上の素数の場合において、解が存在しないことを言えたら終いやー！
と息巻くのは早計です。
なぜなら、そもそも素数という概念すら未知に溢れており、素数の法則や素数を表現する普遍的な数式・理論は存在しないからです。
つまり、人類が未だ発見できていない素数は無限大に存在しているということです。
この事実は、nが3以上の自然数〜という条件よりも難しく複雑と言えるかもしれません。
この素数の壁が立ちはだかったことで、フェルマーの最終定理に取り組む数学者はいなくなりました。
もちろん、いたにはいたのですが、この素数をどう考えるか？という部分が巨大な壁として立ちはだかったのですね。
こうして、フェルマーの最終定理はそれからさらに100年以上の進展がないままだったのです。
しかし、1953年4月11日、イギリスのケンブリッジにて、光の勇者が誕生するのでした…。次回へ続く。
まとめ
今回は、1800年代の数学者たち、オイラー、ソフィージェルマン、ディリクレ、ルジャンドル、そしてラメがフェルマーの最終定理に挑む過程をご紹介しました。
具体的にnの値を当てはめるアプローチをとったわけですが、これでは解決できなかったのですね。
果たして彼らの努力はムダだったのか？というとそんなことはありません。
フェルマーの問題を考えていくことで、問題が持っている性質を明らかにしていきました。
このアプローチで解決こそはされませんでしたが、このプロセスの中に新しい数学的理論が誕生していったのですね。
果たして、天才数学者たちはフェルマーの最終定理をどのように解決していったのでしょうか？
次の記事でご紹介します。
最後までお読みいただき、ありがとうございました！
