どうも、丸田です。
今回はアラビア数学の歴史について解説します。
アラビア数学と聞いてもあまりピンとこないかもしれません。
ですが実は、歴史上において非常に大きな功績を残しているのです!
というかアラビアの数学発明がなければ、下手すると現在の教育カリキュラムに数学が存在しなかったかもしれないと言っても言い過ぎではありません。
では何がすごいのか?
一言で言えば、ギリシャ数学とインド数学が融合し、より実用的になったということです。
画像
このギリシャ数学とインド数学を融合させた「アラビア数学」の発展が、後のヨーロッパ、そして世界全土の数学文化に大きく影響を与え、世界の数学の発展へと繋がっていくことになります。
いわゆる、数学革命です!
ということでアラビアの数学の歴史の詳細と、貢献した数学者を解説していきます。
アラビア数学の英雄現る!
アラビアは元々は何の変哲もない場所だったそうですが(失礼なw)、7世紀からイスラム教が始まり、一気に都市として栄えていきました。
8世紀の中頃には国が栄え、それに従い学芸の文化も栄えたそうです。
そこで生まれたのがアラビア数学という数学文化だったのですね。
そんなアラビアで発展した数学において、英雄と称される伝説の数学者が現れます。
その数学者の名はアル=フワーリズミー。

アル=フワーリズミーは現在のアゼルバイジャンからバクダットへやってきたそうですが、彼の詳細は一切不明です。名前と数学の功績を除いては。
 まるた
まるた正式には、アブー・アブドゥッラー・ムハンマド・イブン・ムーサー・アル=フワーリズミーです。
彼が構築した数学は、一言で言えば”革命”。
数学を実用的なレベルに体系にまとめて、一般の人にも普及させました。
具体的には3つポイントがあります。
- ギリシャ数学とインド数学を融合させた
- 方程式の解法を体系的にまとめた
- 数学を実用レベルにして一般の人にも広めた
これらは数学文化や知恵の風習を大きく飛躍させたのですね。
この数学における大革命こそが、アラビア数学の特色なのですね。
では、ここからは、アラビア数学の英雄アル=フワーリズミーの業績をご紹介します。
1.ギリシャ数学とインド数学を融合させた
当時の数学は、ギリシャでは幾何学、インドでは代数学が発展していました。



幾何学は図形の学問。代数学は方程式という認識でOKです
ですので、図形問題は図形としてのアプローチ。方程式は方程式のアプローチ、という解決策を取ります。
しかし、アル=フワーリズミーはだいたんな発想を思いつきます。



図形と方程式を混ぜちゃえ♡
つまりは、ギリシャ数学とインド数学の融合!
どういうことか?具体的に解説します。
例えば、以下の問題があったとします。
\(x^2+6x=16\)
アラビア流の数学は以下のように解決しました。
まず1辺が\(x+6/2\)の正方形を作ります。
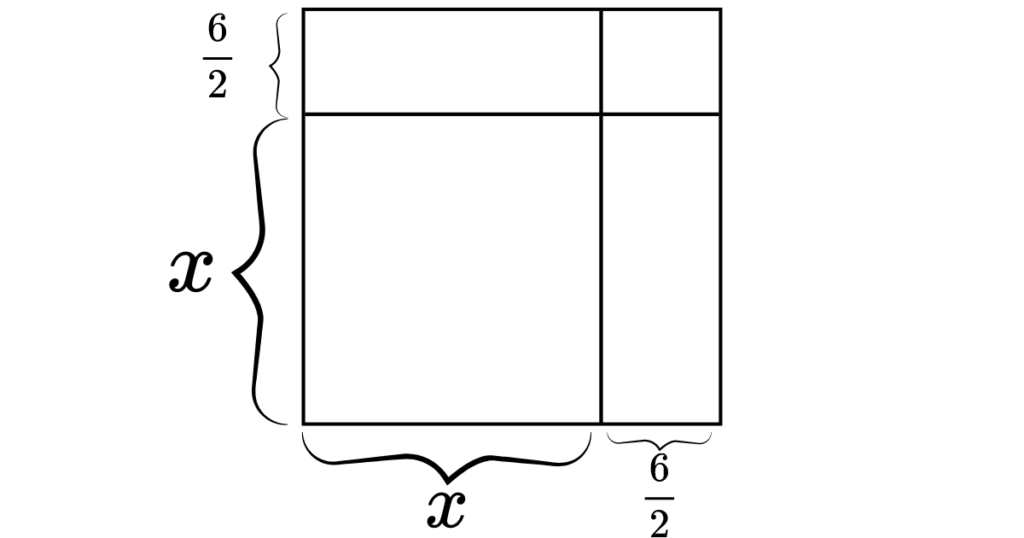

すると面積は以下のようになります。
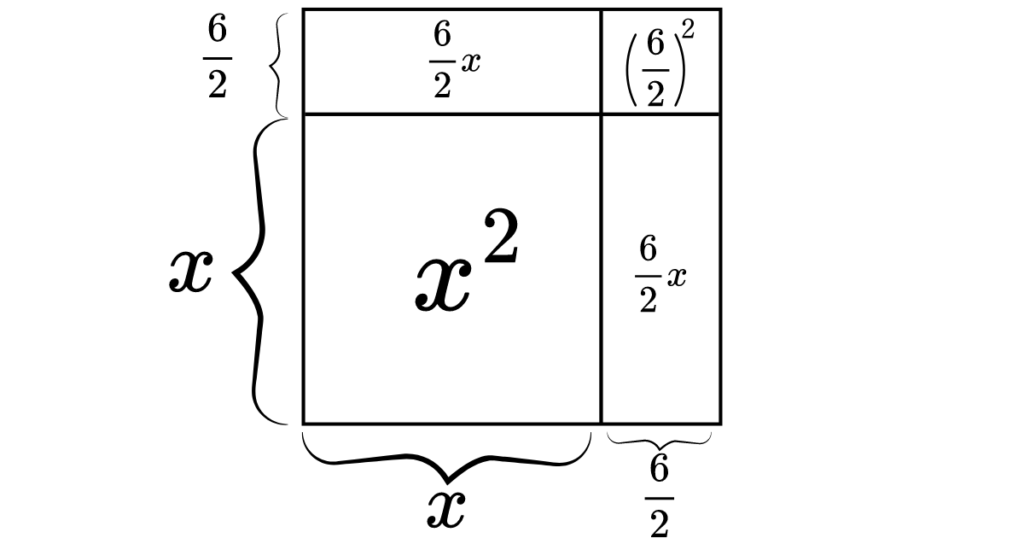

この正方形の面積は全て合わせると、
\(x^2+2×6/2x+(6/2)^2\)
これを計算すると、\(x^2+6x+9\)となります。
もしこの\(x\)が求める解であるならば、\(x^2+6x=16\)なので、\(x^2+6x+9\)に代入して25=\(5^2\)となります。
この25=\(5^2\)は1辺が5の正方形の面積なので、
\(x+6/2=5\)となり、求める解は\(x=2\)となります。
というように、今に比べてはるかにややこしい解法ですが、ここで何がすごいかと言えば、方程式をこのような図形のアプローチで解決できたことです。
この解法には確かに欠点もあります。
- そもそもややこしい
- 解決が大変
- マイナスの解は求められない
などありますが、当時はめちゃくちゃ画期的だったわけです。



クリエイティブは異なる分野の組み合わせといいます。
方程式と図形という異なる分野を組み合わせたアル=フワーリズミーは現代にも匹敵するほどの数学クリエイターだったのかもしれませんね。
2.方程式の解法を体系的にまとめた本を出版!


さらにアル=フワーリズミーの素晴らしいところは、数学の計算を世に広めようとしたところです。
当時の数学は非常に難しく、専門家しか扱えないような敷居の高さがあったそうです。
昔は数の計算ができる人は給料が高かったそうなので、そういった側面からも数学を理解するのは容易ではなかったと考えられます。
アル=フワーリズミーは数学の計算をさらに実用的にしようと、方程式の研究に取り組みました。
ありがたいことに、インドでは数字が0.1.2.3.4.5.6.7.8.9の10種類だけで簡単に表記できるという画期的な方法が生まれました。(これを10進法と言います)
このインドで発明された10進法をアル=フワーリズミーは数の計算に応用することで、はるかに数字の計算が簡単になったのですね。
そして、それら数字の計算方法や理論アル=フワーリズミーは体系立てて1冊の本を完成させました。
その本は「約分と消約の計算の書」という本。
この本は瞬く間に大ヒット!
数学という学問が数学者や哲学者だけではなく、商業や工業、測量など一般からビジネスに役立つ形としても取り入れられていきました。



文明の発展と、その国の人々の知恵レベルの高さは比例します。
アル=フワーリズミーの貢献は、数学にとどまらず、文明発展にも貢献したと考えて間違い無いと思います。
インドでゼロが発見された歴史的経緯の詳細はこちらの記事が参考になります。


3.知恵の館にて大いに活躍した


830年頃、バクダットでは、知恵の館(ちえのやかた)と呼ばれる大きな図書館が建てられました。
ちなみに、当時はアッバース朝と呼ばれるアッバース家によるイスラム帝国が築き上げられていたのですが、マアムーンという人物が創設した研究施設が「知恵の館」なのですね。
この知恵の館によって、アラビア地域にて学問の文化が花開いていきました。
具体的には、アリストテレスやプラトンの哲学、ユークリッドの幾何学などギリシャの哲学書や科学書がアラビア語に翻訳されていくという活動がさかんになったのですね。
その知恵の文化発展の一人として、アル=フワーリズミーも大活躍しました。
アル=フワーリズミーは知恵の館を設立したマアムーンに仕えて、数学、科学さらには天文学などの発展に大きく貢献したのです。
ちなみに、知恵の館は世界中の賢い人たちが集まり、数学や天文学、医学など、多くの分野の知識レベルが発展したと言われており、sin,cosなどの原型となる三角法という手法も確立されていたのですね。
まとめ〜革命的なアラビア数学!〜
今回は、アラビア数学の歴史をご紹介しました。
アラビア数学の英雄アル=フワーリズミーの画期的アイデアには脱帽ですよね。
科学評論家のエサン・マスードによると,「代数学はこれまで考案された最も重要な数学的ツールで科学をあらゆる面で支えている」と述べているのですが、それを大きく発展させたのがアル=フワーリズミーなのです。
アラビア数学はあまり歴史的文献や資料が残っていないため、情報量は少ないのですが、アル=フワーリズミーの業績はもっとすごいものだと想像されます。
では今回は以上です。
最後までお読みいただき、ありがとうございました!
アラビア数学をヨーロッパへ広めた人物は、フィボナッチ数列で有名な数学者フィボナッチです。
詳細はこちらの記事を参考にしてみてください。


PS.当時のアラビアについて
余談ですが、イスラム地域では神の言葉を託された人たちは「預言者(よげんしゃ)」と呼ばれていました。
この預言者としての勤めはノア、アブラハム、モーセ、ダビデ、イエス、そして最後にムハンマドと代々託されてきたそうです。
最後の預言者ムハンマドが亡くなった後に、イスラム国家を指導する最高権威者たちをカリフと称しました。
そのカリフの血筋にマアムーンがいます。
つまりは、アル=フワーリズミーが使えたマアムーンはとてつもなく偉い人だったわけですねぇ。
ちなみに、神が預言者ムハンマドに伝えた言葉が書かれたイスラム教の聖典を「コーラン(正式:アル=クルアーン)」といいます。
もし興味があれば、こちら参考にしてみてください。











