美しさとは何か?
大昔から哲学テーマの1つとして、科学者は美を研究してきました。
1200年頃、イタリアにて。
美しさと数学の関係性を明らかにした数学者がいました。
彼の名は「レオナルド・フィボナッチ」。
彼が発見した数の規則は「フィボナッチ数列」と名付けられ、数学においてとても有名な法則として知られています。
ちなみにフィボナッチ数列は、「黄金比」と密接な関係がある数の規則性です。
フィボナッチ数列は美術や建築、自然現象、さらには金融などにも見られる不思議な性質です。

フィボナッチ数列は、また後ほど解説しますが、美しいとされる神秘の比率「黄金比」を見事に表現した不思議な数の規則です。
また、それだけでなく、植物の成長や自然の流れ・法則、さらには金融市場の動きにまで関わっているという驚きの事実が隠されているのですね!
さて、今回はフィボナッチ数列とは一体何なのか?
またそれを発見した数学者フィボナッチはどんな人生を送ったのか?
この記事では、そのような数学と自然が交わる美しい性質を深く研究したフィボナッチの生い立ちや業績などをご紹介していきます。
数学者フィボナッチの生い立ち
レオナルド・フィボナッチの生い立ちを紹介しています。
アラビア数学を学ぶ
フィボナッチはおよそ1170年頃にイタリアのピサで生まれました。

補足ですが、フィボナッチの本名は、「レオナルド・ダ・ピサ」ですが、父親の名前がボナッチで「フィリオの息子」という意味で「フィリオ・ボナッチ」と愛称がつけられ、さらになまって「フィボナッチ」と呼ばれるようになったそうです。

ややこしいw
フィボナッチは子供の頃から数字が好き過ぎてで、数字のことばかり考えていたそうです。
なので、周りの人たちからは変わり者と思われていたのだとか。
その後、まもなくして父が仕事の都合で移住することに。フィボナッチもついていき、現在のアルジェリアに移住したそうです。
しかし、フィボナッチの数字愛は変わらず、成長したフィボナッチはアラビア数学を学ぶこととなりますが、これがフィボナッチの人生を大きく変えることになります。
フィボナッチはアラビア数学に相当衝撃を受けました。
なぜなら、アラビア数字はヨーロッパ地域の数字に比べてはるかに便利だったからです。
ヨーロッパはローマ数字という複雑な数字体系を採用しておりましたが、実用性にとても乏しい数字体系でした。
例えば、こんな感じです。


数字が増えるたびに、線や記号を増やさなければなりません。




ローマ数字の足し算とかはこんな感じです↓
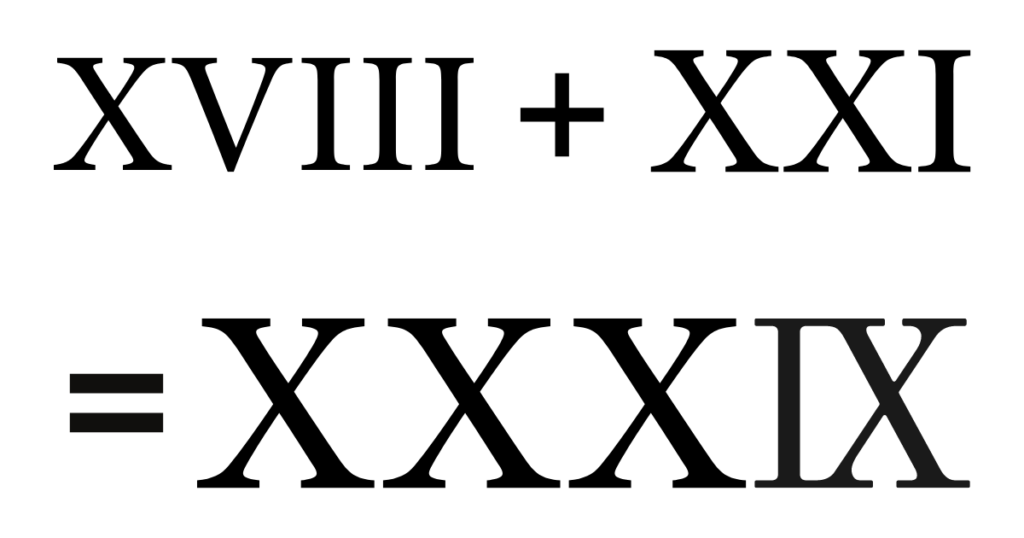
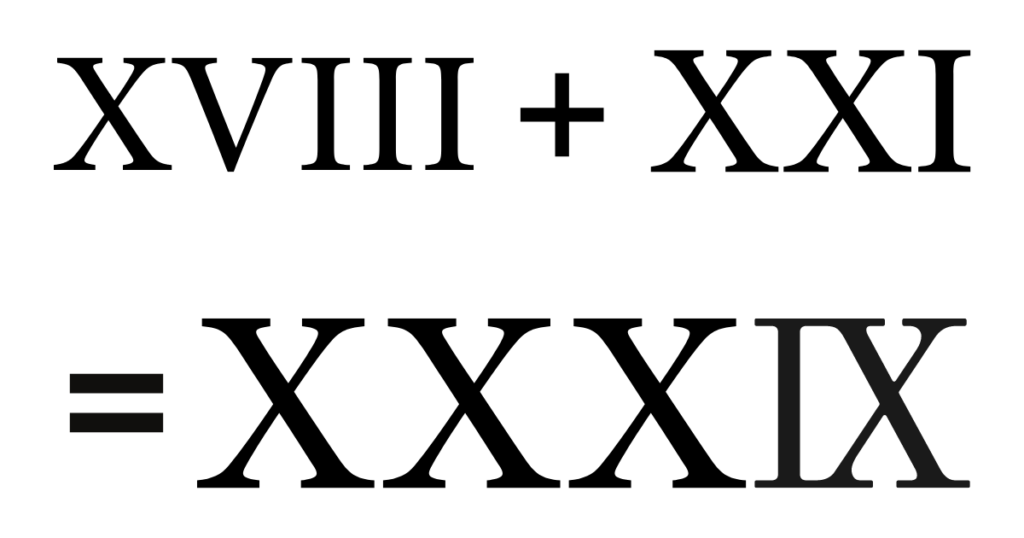
ヨーロッパの数字めんどくさすぎる!!笑
一方、アラビア数学は10進法という「0,1,2,3,4,5,6,7,8,9」の10つの記号だけどんな数字も表現できるという非常に便利な数字体系を活用していました。


アラビアの数字は便利すぎる!!
アラビア数学の数字体系の便利さに気づいたフィボナッチは、さらに数学を深く追求すべく、エジプト、シリア、ギリシアへと数学の旅を歩み始めるのでした。
そして、ここからフィボナッチはヨーロッパの数学文化を大きく開花させることになるのでした。
好きの力は凄まじいですね〜!
「算盤の書」を出版。ヨーロッパに数学を普及させる
フィボナッチは30歳ぐらいの頃に、故郷イタリアへ帰ることとなりました。
さっそくこれまで学んだ数学の知識をまとめた書籍を執筆し始め、1202年ごろに「算盤の書」と名付け出版。
この本が大ヒットしました。
フィボナッチの本は何が凄かったのかというと、数学を実用的な学問に落とし込んだということです。
昔から数学は専門家のための難しい学問とされており、専門家以外の人たちは数字の計算知識すらなく、数学へはノータッチという状況でした。



世界のどこの国でも同じ傾向があります。
特に当時のヨーロッパは「数学は無意味だ」という風当たり強い時代だったこともあり、人々が数学に触れる機会はほぼなかったそう…。
そんな時代に、フィボナッチの本がきっかけとなりヨーロッパに数学が普及していったのです。
フィボナッチが出版した「算盤の書」はアラビア数字を使った計算技法が体系化されており、簿記や利子計算、会計学などに応用できる内容でした。
これにより専門的な人だけでなく、ビジネス現場でも数学が大活躍したのでした。
アラビア地域でも数学を実用的に広めた「アル=フワーリズミー」という数学者がいます。
フィボナッチはおそらく、この時代の数学を引き継いだのではないかと考えられます。
フィボナッチ数列の発見
その後、さらにフィボナッチの進撃は続きます。
数学史でもミステリアスな性質を持つ「フィボナッチ数列」を発見したのでした。
フィボナッチをさらに有名にした発見が「フィボナッチ数列」です。
発見のきっかけは、うさぎでした。笑
フィボナッチは「2匹で1組のうさぎが1年でどれだけ繁殖するだろうか?」という、なんとも可愛らしくて面白い問いに注目したのでした。
しかし、この問いには森羅万象の秘密が隠されているのではないか?と感じるほどの神秘の法則が眠っていたのでした。
この問題は「フィボナッチのうさぎ」と呼ばれています。
はじめは1組。1ヶ月後は1組。2ヶ月後は2組。
3ヶ月後は3組。4ヶ月後は5組。5ヶ月後は8組。6ヶ月後は13組と増えていくことがわかりました。
ちなみに、1年後は144組。
ぐーんと一気に伸びていくわけですね。
しかし、この増えていく数字を並べると実に不思議な性質が浮き彫りとなっていったのでした。
1.1.2.3.5.8.13.21.34…と続く数字の規則はとても神秘的で、人が美しいと感じている「黄金比」と密接な関わりを持っているのですね。
この数字の規則の発見によりフィボナッチはますます有名になっていきました。
その黄金比の研究にさらに新たな要素を見出したことから、フィボナッチはますます高い評価を受けます。
さらにその後、さまざまな数学の研究を続け本を出版。
この功績に注目したのが、当時の皇帝の人々、そして国王のフリードリヒ2世でした。
フィボナッチはフリードリヒ2世からとても気に入られて、宮殿に仕えるようになりました。
フィボナッチは行政や課税、大学設立など、町の活性化における数学的アドバイスをする役職に勤めたそうです。



まさにデータサイエンティスト!
こうして1250年頃まで、フィボナッチは自らの使命を全うして生涯を終えたのでした。
数学や科学の貢献が認められピサ共和国から表彰もされ、フィボナッチの像も建てられています。


引用:https://4travel.jp/travelogue/10782657
数学者フィボナッチの生涯と功績について
今回はイタリアの数学者、レオナルド・フィボナッチをご紹介しました。
フィボナッチ数列で有名な数学者ですが、それだけではなく、アラビア数学をヨーロッパにも輸入して、ヨーロッパの数学文化を盛り上げたという数学史においても非常にすごい貢献をしているのですね。
フィボナッチの活躍のおかげで、ヨーロッパでは次々と新しい数学の定理や法則が発見されていくようになります。
フィボナッチは、まさにヨーロッパの数学ブームを作ったと言っても過言ではありません。
黄金比やフィボナッチ数列はさまざまな分野にも応用されております。
より詳しく知ってみたい方はぜひ調べてみてください。とても面白いと思いますよ。
では今回は以上で終わります。
最後までお読みいただき、ありがとうございました。
フィボナッチが発見した、フィボナッチ数列について解説しております。
ぜひ参考にしてみてください。











