どうも、丸田です。
今回は幾何学の父、ユークリッドをご紹介します。

ユークリッドは数学業界にとてつもない影響を及ぼしている人物で、「ユークリッド空間」や「ユークリッド距離」「ユークリッド幾何」など、彼の名前が使われてる概念はいくつも存在します。
またユークリッドは数学の定理をまとめた「原論」を出版しており、この本なんと世界で2番目に売れているのです。
 丸田
丸田まさに数学界の大ベストセラー!
1番は聖書ですから、原論は数学版「聖書」と言っても過言ではありません。
また別名「幾何学の父」とも呼ばれており、幾何学という数学の学問を厳密に、体系化した偉大な人物なのです。
そんな数学の神とも呼べるユークリッドはどんな人生を送ったのか、また原論は一体何が凄いのか。
その秘密に迫りたいと思います。
ユークリッドの生涯
勉強に励んだ少年ユークリッド
舞台は紀元前330年頃。シリアの片田舎にユークリッドは生まれました。
ユークリッドの家庭はとても勉強熱心で、特にユークリッドの父は勉強面において心配ばかりしていたそうです。





親が子の勉強を心配するのは、どの時代も変わらないのが興味深い
その影響を強く受け、ユークリッドは勉強に打ち込みます。
そんな生活を送る中、ユークリッドは父からこのように言われました。



シリアでは何も学べん!
ギリシャのアテネに行くがよい
当時のアテネは、プラトンの設立したアカデメイアによって哲学や自然科学、天文学など、知識の文化で賑わっていました。
だからこそ、父は「勉強するならアテネだろ!」と思い、提案したわけですね。
ユークリッドはその提案を受け、アテネへ向かうことに。
そこでプラトンの学びを受けた様々な哲学者、数学者、科学者と一緒に長いこと勉強したのでした。
ユークリッドは幾何学への理解を深め、研究に打ち込みます。
彼の才能はメキメキと発揮され、ギリシャの国中にユークリッド名は広がっていったのでした。


【参考記事】プラトンに関する記事はこちら
哲学者プラトンとは?功績やアカデメイアについて
大学校の講師として招かれる


その頃、エジプトの都市アレクサンドリアでも知識の文化が大変賑わっていました。
というのも、アレクサンドリア都市を治めていたプトレマイオス一世は都市に大学をはじめ、図書館や動物園・植物園、実験所などを建設していたのです。
このような経緯で、アレクサンドリアにも科学や知恵の文化が浸透してきていました。
プトレマイオス一世はユークリッドに着目し、アレクサンドリア大学の講師として招くことにしました。
ユークリッドはアレクサンドリア大学の講師としても大活躍し、さらに名前は知れ渡ることになるのでした。
ユークリッドが大学で教えたテーマはもちろん「幾何学」。
難解なテーマでしたが、しっかり教えることができたそうです。
幾何学はとても難しい学問でしたが、どれぐらい難しいかと言えばプトレマイオス一世も音を上げるほどだったそうです。
プトレマイオス一世は「ユークリッドよ。幾何学はどうも難しい。どうにかして楽な勉強方法はないものかね」と尋ねたそうですが、
ユークリッドはバシッと、「王よ!幾何学に王道はありませんぞ!」と発言したそうです。
これはユークリッドが幾何学をいかに重要視していたかが垣間見える有名な逸話です。



さすがユークリッド!!王にすら堂々と発言するなんて!
おれたちにできない事を平然とやってのけるッ
そこにシビれる!あこがれるゥ!
原論を出版。最期まで研究を続ける使命に燃える男!


紀元前300年頃に「原論」が出版されました。
原論とは数学の定理をまとめた書籍なのですが、これがもう売れに売れました。
現在では売上No.1の聖書に次いでNo.2です。
とてつもなく売れています。
ちなみに、てこの原理や浮力を発見したことで有名な科学者アルキメデスも原論を愛していたそうです。
3〜5世紀頃は、エジプトで広がり、8〜10世紀には、アラビア語に翻訳され、アラビア数学に浸透。
11〜12世紀には、ラテン語に翻訳されヨーロッパに伝承されていきました。
このようにそれでも世界中に普及したのは凄まじいですよね。
しかもその頃、著者のユークリッドは30代の頃。
いかにユークリッドが天才だったかがわかるエピソードですよねぇ。
原論には数々の数学の定理がまとめられています。
原論は全部で13巻で構成されており、内容をザックリご紹介すると以下の通りです。
1巻〜4巻:三角形、面積、円、正方形などの図形の性質
5巻〜6巻:比率、幾何学の比例、相似、黄金比
7巻〜10巻:数列、素数、最小公倍数、最大公約数、平方根(ルート)
11〜13巻:円の面積、球の体積、立方体、六面体、円錐、円柱、角柱、角錐、正多面体などの立体
これだけの数学に関する性質が原論には、たっぷりと掲載されているのですね、
この原論は別名「エレメント」と呼ばれるのですが、今現在も使われているそうです。
(若干、変更は加えられていますが、内容の根幹はあまり変化なし)



紀元前に発見された定理が現代にも通用するとは、かなり普遍的な内容だったことがわかりますね。
他にも、幾何学や数論、素数に関する研究をし続け、ユークリッドは紀元前275年頃まで生きたと言われております。
ユークリッドの残した「原論」について
ユークリッドは生涯に数々の業績を残しましたが、「原論」が一番有名です。
では、「なぜ原論はそこまで凄いのか?」を解説していきます。
結論からいうと、原論のスゴさは数学の「公理(こうり)」というものを明確に定めたことにあります。
聞き慣れない言葉かと思いますが、簡単にいうと「論理の前提」です。
数学の特徴は論理を積み重ねて、様々な定理や公式を発見していくことです。
ですが、どれだけ厳密な理論を積み重ねても、一番最初の土台が間違っていれば、その理論は意味がありませんよね。
現代の数学という学問を1本の木に例えるなら、「定理」が葉っぱ、「定義」が木、「公理」が土みたいなイメージです。
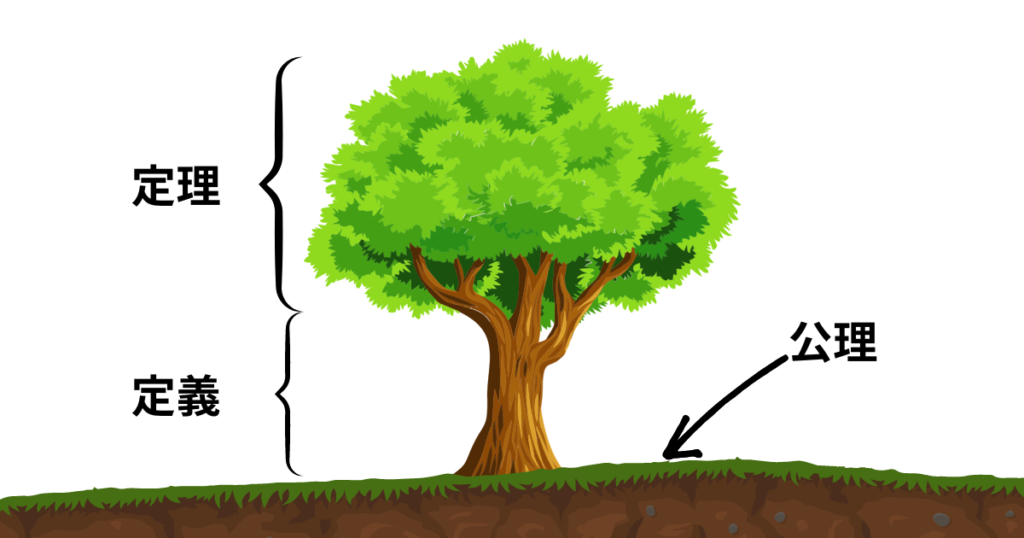

土がしっかりしているから、木が元気に育ち、木が育つから緑が生まれます。
それと同じで数学は、厳密な「公理」を決め、「定義」をしているから、いろんな定理が生まれるし、その定理を信頼することができるのです。
しかし、当時はそのような考えを持つ者はいませんでした。
そんな中、ユークリッドは数学の論理においても、確固たる土台が必要だと気づいたのですね。
この数学の土台を固めたのが原論なのです。
この公理が定まったことが、数学そのものの論理の安定性を高めたのですね。



なるほど。そりゃ原論売れるわな
特にユークリッドは幾何学に精通していたので、幾何学に関する5つの公理を定めました。
(※公理は昔は「公準」と呼ばれました)
以下、ユークリッドの公理(=公準)です。
- 任意の2点が与えられたとき、それらを端点とする線分を引くことができる。
- 与えられた線分はどちら側にでも、いくらでも延長することができる。
- 与えられ任意の点に対し、その点を中心として任意の半径の円を描くことができる。
- すべての直角は互いに等しい。
- ある直線が他の2直線と交わるとき、同じ側の内角の和が2直角より小さいならば、この2直線は限りなく延長された時、内角の和が2直角より小さい側で交わる。
まぁぶっちゃけ、この公理(公準)の内容自体は「当たり前じゃね」と思えるような内容です。
ですが、公理を定めることは非常に難しいのです。
なぜなら、公理(=公準)は、論理の大前提の部分であり、証明ができないからです。
例えば、「京都に行くなら飛行機を使いましょう(主張)。なぜなら、早くついた方が、いろんな場所を巡ることができるからです(根拠)。」は論理的ですね。
普段から、我々はこのような思考や会話をしています。
しかし、論理の大前提となる公理とは、「主張」しか存在しません。
だからこそ、公理(=公準)は100人中100誰が「異論なし!」と言えるような超厳密に、め〜ちゃくちゃ慎重に定める必要があったのです。



ここで公理を間違えれば、この先何千年先の数学が崩れ去ってしまうのです。
公理を定めるという、大偉業を成し遂げたのがユークリッドなわけですよ。
ユークリッドが定めた公理は、現在に至るまでさまざまな数学者が反論がないか調べ尽くしているのですが、2000年以上にわたり、公理に誤りはないと考えられています。
※1800年代からユークリッドの公理を否定して生まれた非ユークリッド幾何学という学問が生まれています。
【補足】公理は現代社会でも応用できる
公理の考えは現代社会にも応用できる側面があります。
例えば、あなたがもし友達と旅行で京都に行くとします。
「京都に行くなら現地に早く着く飛行機を使った方が良い。なぜなら、現地に早くついた方が、いろんな場所を巡ることができる。」
と言ったとしましょう。
上記の主張には「いろんな場所を巡ることが良い」という前提が存在します。
しかし、「京都へ行くまでの道中も楽しむべきだ」という前提がある友人は「いやいや、別にバスで良いんじゃない?あるいは車でもいいじゃん。」と主張するかもしれません。
これは超ザックリで雑な例ではありますが、
他にも「どうすれば幸福になれるか?」「好きなことして生きていくには?」「素敵な恋愛がしたい」
などなど、様々な考えや主張、議論もそもそもの大前提がズレていれば話が平行線になることも少なくありません。
そんな状況を解決するのが、前提を揃えるということなのです。
そういった意味では、前提を意識することはとても大切であり、数学の公理への考え方は実社会にも役立つ側面があるのです。
幾何学の父、ユークリッドの功績と生涯、原論のまとめ
今回のユークリッドの功績と生涯、原論について解説しました。
ユークリッドが原論で定めた「公理」がとにかくすごい!と言うことが伝わっていれば嬉しいです。
ユークリッドが紀元前に築き上げた幾何学の基本的原理や公理は、現代でも幾何学の基盤となっております。
だからこそ、現代の数学者は安心して定理を導き出せるわけですね。
数学界の幾何学の父、そして大ベストセラー作家ユークリッドの解説を終わります。











