どうも、丸田です。
突然ですが、学生の時を振り返って「なんであんなに図形の勉強してたんだっけ?」って思いません?
たとえば角度や、辺の長さ、面積を求めたりしていたわけですが。
そもそもなんで?いつ使うん?
謎ですよね〜。
そこで数学の歴史を調べて、紐解いて見た結果、面白い事実が浮き彫りになりました。
ということで、今回は幾何学の歴史をご紹介します。
図形の学問(=幾何学)の始まり
幾何学はなんと紀元前3000年頃から始まったとされています。
なぜ幾何学が発展したのか?
その理由はズバリ!「生きるため」です。
決して賢く生きるとか、自分らしく生きよう!とか。そんなチャチなもんじゃあ断じてありません。
物理的に生きる。生き延びるためなのです!

それを理解するために、少しだけ人類の起源の話をします。
人類は太古の昔、大きな川の近くで栄えました。
- エジプトのナイル川
- バビロニアのチグリス・ユーフラテス川
- インドのガンジス川
- 中国の黄河・長江
これらは古代四大文明と言われたりしますが、文明は大河を起点として栄えていったというわけです。
 まるた
まるた中学の社会で習った内容です。懐かしい〜
なぜ河川の近くなのか、それは水資源が豊富だから。
そのため、当時の人たちは川から取れる水の恩恵を多分に受けていたのですね。
畑を育てたり、必要は水分確保に、川は大変ありがたい存在でした。
しかし、デメリットもあります。
それが河川の氾濫。


川が氾濫すると、ものすごい勢いで水があらゆるモノを飲み込んでしまいます。
命に関わる危険性もありますし、せっかく一生懸命育てた作物などが全部ダメになってしまうのですね。
そこで街を治める人たちは、洪水対策を強いられ、また洪水によって失されてしまった、田んぼの損害賠償の計算をし、再び引き直す必要に迫られた
こうして土地測量術が進歩していったのでした。
これが幾何学の始まりなのです。
※幾何学の理論は、エジプト周辺から始まったとされています。
ちなみに、幾何学は英語で「geometry(ジオメトリー)」ですが、「geo」は土地、「metry」は測量を意味します。
土地の測量するのに縄を用いていました。
そのために、土地測量の専門家たちは、「縄張り」と呼ばれていました。
直角に命をかけた古代数学者たち
では具体的に幾何学を用いて、何をしていたのか?
それは「直角」を作り出すではないかと考えられています。


この「直角」は主に、建物の建設における安全性を飛躍的に高めてくれます。
想像するとわかりやすいですが、今住んでいる家の角がよく見たら直角じゃなくて、少し斜めっていたらヤバいですよね笑
シンプルに倒壊する危険性があります。
大昔の時代は、人々の家を建てるほか、神殿を築いたり、塔を建てたりと大きな建造物も多かったため、より一層建物の崩壊リスクを下げる意識が大切でした。
そういった時代背景もあり、古代の数学者たちは、「直角」を作り出すことに命懸けだったのでは無いかと考察できるのです。
補足ですが、現代のように分度器も定規もないため、直角を簡単に作図することは難しいです。
またフリーハンドや感覚で、直角を作るのも至難の業です。
古代の数学者たちが「直角」を重要視していた根拠を述べていきます。
三平方の定理
幾何学で有名な定理に「三平方の定理」という定理があります。
別名「ピタゴラスの定理」と言われており、紀元前の数学者ピタゴラスが証明した定理です。
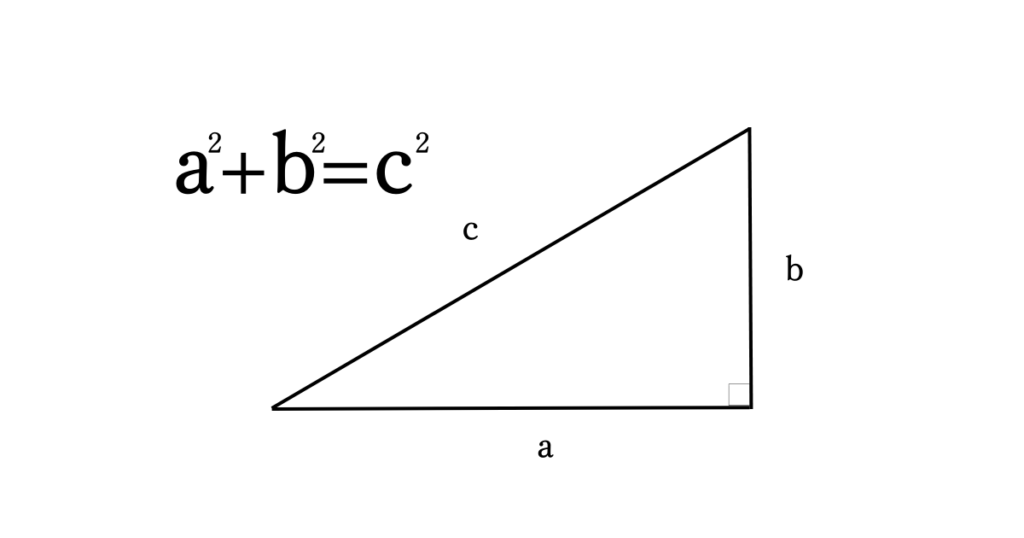
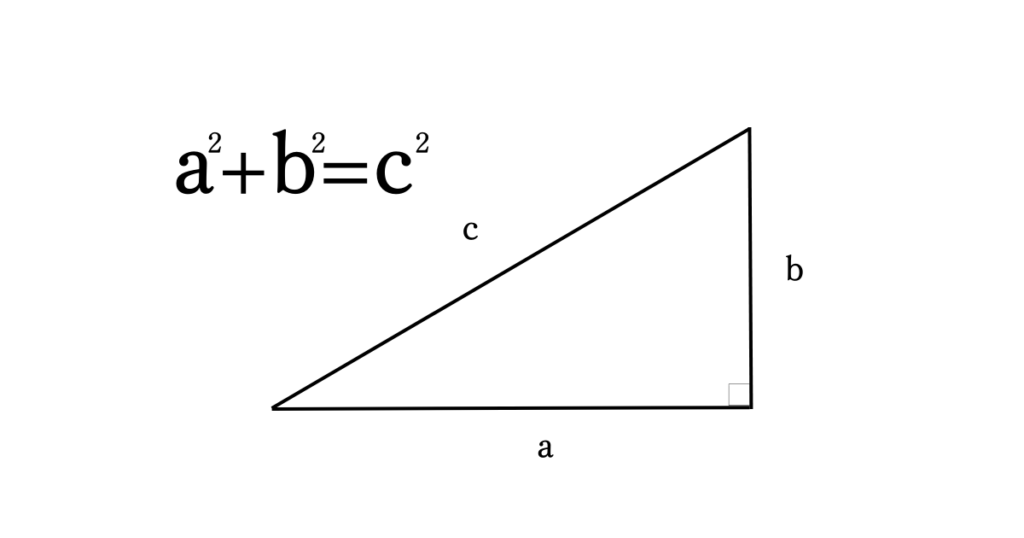
\(a^{2} + b^{2} = c^{2}\)となるならば、三角形は直角になる。
または三角形が直角ならば\(a^{2} + b^{2} = c^{2}\)となる
この定理を証明したのはピタゴラスですが、実はピタゴラスが証明するよりも2000年以上も前から「三平方の定理」は存在していたそうです。
要するに、ピタゴラスは理論的に「三平方の定理」の正しさを証明したわけですが、さらに大昔の人たちは感覚的に三平方の定理を知っており、使っていたわけです。
その理由が、建物の安全性を高める「直角」を作り出すためだと考えられるのです。
おそらく、いろんな直角を作るテクニックを模索した中で、「お!こうすりゃ直角できるじゃん!」と発見した人がいたのでしょう。
その発見がいわゆる「三平方の定理」と呼ばれているものだったと考えられます。
「親方!なぜこの長さにすると、直角になるんですか?」「ばかやろー!考えるな!感じろ!」
的なやり取りがイメージできますね笑(俺だけかw)
先ほども補足したのですが、フリーハンドで直角を作るのは至難の業です。
僕は大学時代は、建築学科だったのですが、フリーハンドで完璧に直角を書いたつもりが盛大にズレていた経験があります笑
だからこそ、大昔の人たちは建築を通して、直角になる辺の関係性を経験から編み出したのではないかと思うのです。
円と直角の関係「タレスの定理」
直角が重要であった証拠は他にもあります。
それが一番最初の哲学者・数学者と言われる「タレス」が証明した定理です。
中学では円周角の定理と学びますが、別名「タレスの定理」です。
円周角の定理とはこういう定理です。
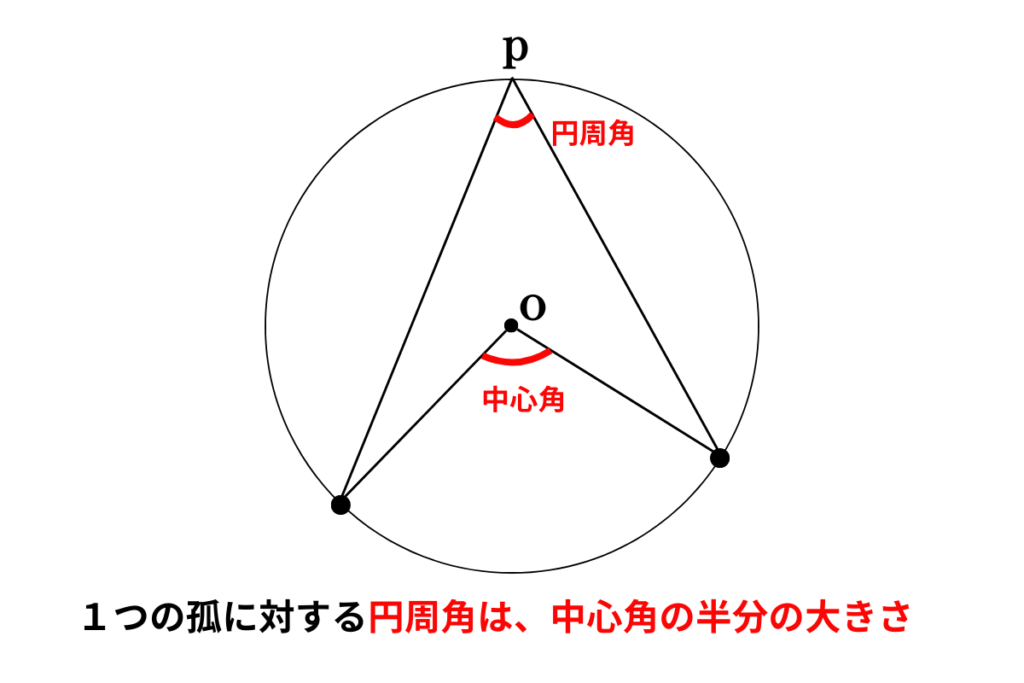

※他の性質もありますが、気になる方はぜひ調べてみてください。
「1つの孤に対する円周角は、中心角の半分の大きさである」という性質を応用すれば、以下のように直角を作り出せてしまいます。


なぜなら、直径にできる180が中心角となり、直径の2つの端から円上の点を結んでできる円周角は180の半分の90度になるからです。
つまり道具が少ない時代において、円を書いて直径と円上の点を結べば直角が作れるのはさぞ便利だったのではないかと思うのです。
そうなると、次なるミッションは「どうやって綺麗な円を書くか?」という円という概念への研究です。
ここで円を円たらしめる重要な概念「円周率」が研究され始めたのではないか、と考えています。



円周率の計算も、紀元前の昔から行われていました。
とはいえ、アルキメデスが登場するまでは、円周率は”3”とされていたと言われています。
以上で、考察は終わりです。
最後にどのように幾何学の理論が現在へと語り紡がれてきたのかを解説して終わります。
リンド・パピルスで後世へ伝わった幾何学の叡智たち
古代エジプトでは河川に水草が生い茂っていたのですが、この一部から紙を作って文章を書いていました。
その文章の紙を「パピルス」といいます。
英語「paper」の語源です。
紀元前1650年頃にエジプトの僧侶アーメスが、パピルスに幾何学の知識や定理を書き記していたのですが、このパピリスを1858年頃、考古学者リンドが見つけました。



グッジョブ!リンド!
そして、解読した結果、さまざまな数学の定理が記載されていたことが判明。
主に面積や体積を求めたり、二等辺三角形や、台形、円周率円の面積、立体、角錐、正四角錐、ピラミッドの形の幾何学を解き明かす数々の定理が記載されていたのです。
これが学生時代に学んだ幾何学の始まりだったのですね。
とはいえ、当時のエジプトの幾何学は現場勘で培った感覚的な法則が多く、確固たる理論性や正当性がありませんでした。
これら幾何学を厳密に証明し、論理を加えたのが、タレスやピタゴラスなのですね。
まとめ
今回は、幾何学の歴史をご紹介しました。
都市の繁栄、建設技術、土地の測量など、まさに生きるため、生活の質を高めるための知識だったのですね。
学生時代に学んでいた幾何学の成り立ちを知ると、深みが生まれますよね〜。
ぜひ興味が湧いた方、中学の幾何学を復習するのも一興かもしれませんよ!(中学の図形はけっこう難しい!笑)
少しでも、数学おもしろ!と感じていただけたなら、幸いです。
最後までお読みいただき、ありがとうございましたー!











