どうも、マルタです。
あなたは「モンティ・ホール問題」をご存知でしょうか。
簡単に言えば、「どちらが合理的か?」を問う確率の問題です。
内容は非常にシンプル。しかし「多くの数学者に赤っ恥をかかせた」と言われるほどの頭を悩ます難問です。
しかも!
面白いことに、この問題を考えたのは数学者ではないのですね。
アメリカのテレビ番組「Let’s Make a Deal」の司会者「モンティ・ホール」が生み出しました。
 マルタ
マルタ故に、モンティホール問題
モンティホール問題で分かることは、ズバリ「直感はあてにならない」ということです。
では、そんな多くの数学者を混乱させたモンティホール問題とは一体何か、について解説していきます。
ぜひ一緒に知的好奇心を満たしていきましょうー!
モンティ・ホール問題とは
モンティホール問題の内容をお伝えします。
3つの扉があります。
1つの扉の先には「クルマ」。残り2つの扉の先には「ヤギ」がいます。
あなたは1つだけ扉を開けることができ、もしクルマを当てたらプレゼントという、なんとも太っ腹な企画です。
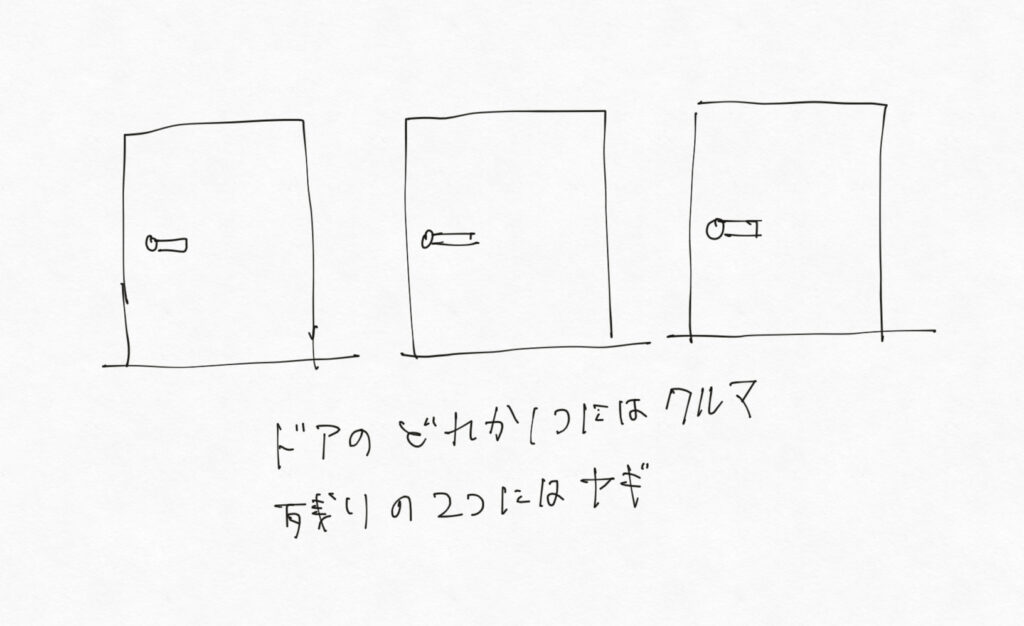

「さぁ、3つの扉のうち、あなたはどの扉を開けますか?」という問題です。
が!
大事なポイントはここから。
あなたが3つの扉のうち1つを選びました。
すると、次にあなたはこう言われます。
「今からハズレの扉を1つだけ開けます。その後に、あなたは最初選んだ選択肢を変えても良いです。
さてあなたは選択肢を変えますか?変えませんか?」
果たして、クルマが当たる確率は【変える】、【変えない】のどちらが高くなるでしょうか?
というのが、モンティ・ホール問題です。
さて、あなたならどうしますか?
よければ少し時間を空けて考えてみてください。
ちなみに、僕は選択肢は変えませんでした。
なぜなら、最初選んだ扉がアタリである確率は1/3で、変えても変えなくても確率は変わらない。ゆえに変える必要はないと思ったからです。
もしかしたら、あなたもそう考えたのではないでしょうか?
答えは最初の選択肢を変えるとアタリである確率が高まるのでした。
しかもアタリの確率が2倍にハネ上がるのです。
つまり、最初選んだ選択を変えるとクルマが当たる確率は2/3になる、というわけなのですね!
モンティ・ホール問題の具体的な解説


では、なぜ選択肢を変えるとアタリの扉を引く確率が2/3になるのか?解説していきます。
ここで重要なのは、扉を1つ選んだのちにハズレが1つ明らかになるということです。
もし選択肢を変える場合、2つのシチュエーションが考えられます。
①最初にアタリの扉を選んだ場合
②最初にハズレの扉を選んだ場合
①最初にアタリの扉を選んでいた場合
もしあなたが、最初にアタリの扉を選んでいた場合。
次に選択肢を変えたら残念ながらハズレです。
そう考えると、「変えても意味なくね?」と思うでしょう。
ですが、よくよく考えてみると、そもそも最初にアタリを当てる確率は1/3。
一方、最初にハズレを引く確率は2/3なので高い確率でハズレてしまいます。
なので、最初でアタリを引けた場合は、それはただのラッキーだったというわけです。
②最初にハズレの扉を選んでいた場合
一方で、最初にハズレの扉を選んでいた場合、選択肢を変えれば必ず当たります。
なぜなら、あなたが引いたハズレの扉とは別の扉が開くからです。
ということは、あなたが選択肢を変えたなら、それは間違いなくアタリの扉だというわけです。
ここで最初にハズレの扉を選ぶ確率は2/3です。
これは最初にアタリを引くよりも高い数値ですよね。
しかし、その次に選択肢を変えたなら、もう一つのハズレの扉が開き、残る扉はアタリのみになります。
つまり選択肢を変えると確実にアタリになるということです。
仮にハズレの扉をそれぞれハズレ1とハズレ2と区別したとします。
ハズレ1をあなたが最初選んだら、ハズレ2が開きます。その後で選択肢を変えれば、アタリの扉を開けることができるということです。


同様に、最初ハズレ2を選んだとしても、ハズレ1の場所が明らかになるので、その後、選択肢を変えれば確実にアタリを引くことができるのですね。


あなたが最初にハズレを引く確率は2/3。
選択肢を変えれば、その確率がそのままアタリを当てられる確率になるのですね。
実際にモンティ・ホール問題をやってみた結果…
とはいえ、「それって机上の空論だろ!?」と思うでしょう。
こういう問題は体験してはじめて分かるものです。
その気持ち、よくわかります…。
ということで、実際にやってみました!w
助手の奥さんに手伝ってもらった結果…。
最初の選択を変えなかった場合、10回中5回アタリ
最初の選択を変えた場合、10回中6回アタリ


………って、おいー!笑
結果が変わらなすぎて、全然わかんねぇ〜!!どれだけ運良いんだよ!!
これじゃ取れ高がねぇぜ…。
※実際に、モンティ・ホール問題をやった時の動画です
ということで、
もっとサンプル数を増やさないと!と思いまして、こちらのサイトで検証しました。
このサイトではモンティホール問題の試行回数を何万回も試すことができます。
他にも便利なツールが掲載されているので、ぜひ見てみてください。
さて、そのサイトでモンティホール問題を10万回やってみました。
その結果、選択肢を変えない場合の確率はほぼ1/3。


選択肢を変えた場合の確率はほぼ2/3になりました。


ということで、実際にやってみてもモンティ・ホール問題の理論は正しいことが証明されたかなと思います。
まとめ 〜モンティ・ホール問題が浮き彫りにしたもの〜
ということで今回は、モンティ・ホール問題について解説しました。
数学や雑学が好きな人には、とても興味をそそられる思考実験だったのではないでしょうか。
この問題が浮き彫りにしたことは、「いかに人の直感はあてにならないか」です。
もちろん、直感に頼ることが悪いことではありません。
ただ確率論的には大きく外れる傾向があるということです。
おそらく、最初の選択肢を変えなかった人が多いのではないかと思います。
それも「なんとなく」や直感で「変えても確率は変わらんやろ」と思ったのではないでしょうか。
ですが、じっくり考えてみると変えた方が確率が高まるという結果だったのですね。
僕らが普段行っている行動が果たして、確率論的に合理的なのか?を見直してみると面白いかもしれませんね。
補足
モンティ・ホール問題を数式で解説している動画がニコニコ動画であるので、ぜひこちらも参考にしてみてください。







