今回は、数学の神童と讃えられたフランスの数学者、科学者、思想家パスカルをご紹介します。
パスカルという男の生涯を一言で言えば、”人生2度生きた神童”です。
パスカルは幼い頃から天才でした。
その天賦の才をあらゆる分野で発揮し、数学だけでなく、物理学、哲学、さらには発明、実業などでも大きく活躍しました。
いわゆる、オールマイティというやつです。
西武ライオンズの野村克也元監督が、田中将大投手に対して「マー君、神の子、不思議な子」と褒め称えたように、僕はパスカルを「パスカル、神の子、不思議な子」と讃えたい気持ちでいっぱいです。
しかし、晩年には思想家に転身。キリスト教に深く傾倒し、その普及活動に精力的に活動し始めます。
これってもしかしたら、「科学者が異世界転生したら宗教家だった件」とか作品作れるんじゃないですかね笑
しかし、39歳という早すぎる死を迎えました。
濃い!実に密度濃い人生ですよ。
さて、そんな神童パスカルは一体どんな人生を送ったのでしょうか。また数学にどんな業績を残したのでしょうか。
その詳細に迫ってまいります!
パスカルの生い立ち

神童の誕生
パスカルは1623年、フランス中部の町、クレルモン・フェランに生まれました。
税務官の父エチエンヌと、母アントワネット、姉ジルベルト、妹ジャクリーヌの5人家族で裕福で明るい家庭に育ちます。
まさに、文句なしの幸せ一家。
と思いきや、2つの不幸が彼を襲いました。
まず1つ目は、彼はとても虚弱体質であったこと。この体質によって、彼は生涯苦しめられることになります。
そして、2つ目が、パスカルが3歳の頃に母親がなくなってしまったことです。
このように幼い頃から、人生にはかげりが見え始めていたパスカルですが、逆境に負けずに彼は才能を開花していくのです。
パスカルが8歳の頃に、一家はパリへ。
実はパスカルの父エチエンヌは、アマチュア数学者でもあり、自宅にはしばしば学者や知識人を招いては、数学や自然科学などについて議論していたと言われています。
小さなパスカルは、そんな大人たちの知的会話を壁越しに聞きながら、自然と科学に興味を抱くようになります。
エチエンヌはとても教育熱心で、パスカルにはいろんな教養を教え込みました。
ですが──1つだけ特殊な教育方針がありました。
なんと父エチエンヌは、「数学は、15歳になるまで学ばせない」としていたのです。
あれだけ自分が数学好きなのに? と不思議ですよね笑
どうやら、エチエンヌは、幼い頃から難しいことを考えすぎるのはよくない。
まずは幅広い基礎知識から身につけるべきだ、と考えていたそうです。
人によっては数学に一度ハマると抜け出せない中毒性があるため、
もしかしたら、子供に数学は刺激が強すぎる、と考えていたのかもしれません。
エチエンヌは想像以上に徹底しており、家の中から数学書をすべて撤去、パスカルに“数学禁止令”を言い渡したのでした。
しかし、人間は禁じられると、かえって知りたくなるもの。
お互い会うことを禁止されたロミオとジュリエットが、かえって恋心を燃え上がらせるように、数学を遠ざけられたパスカルもまた、強く惹かれていきます。
パスカルは父にバレないように、ひっそりと幾何学の勉強します。
そんなハラハラした日々が続く中、パスカルが12歳のとき。
彼はなんと独学で「三角形の内角の和は180度」という定理を発見してしまいました。
誰にも何も教わらずに、自力で導き出せるのが、すでに天才のそれです。
これには父エチエンヌも脱帽。
ついに“数学禁止令”は解除されたのでした。
そして、エチエンヌはパスカルに多くの数学書を買い与えてくれるようになったのでした。
パスカルの快進撃、始まる!
パスカルは数学を教科書を読むことを許されたため、数学でも超有名なユークリッドの古典「原論」を読み始めたそうです。
そして、16歳にして初の論文を発表しました。
【業績1】円錐曲線試論
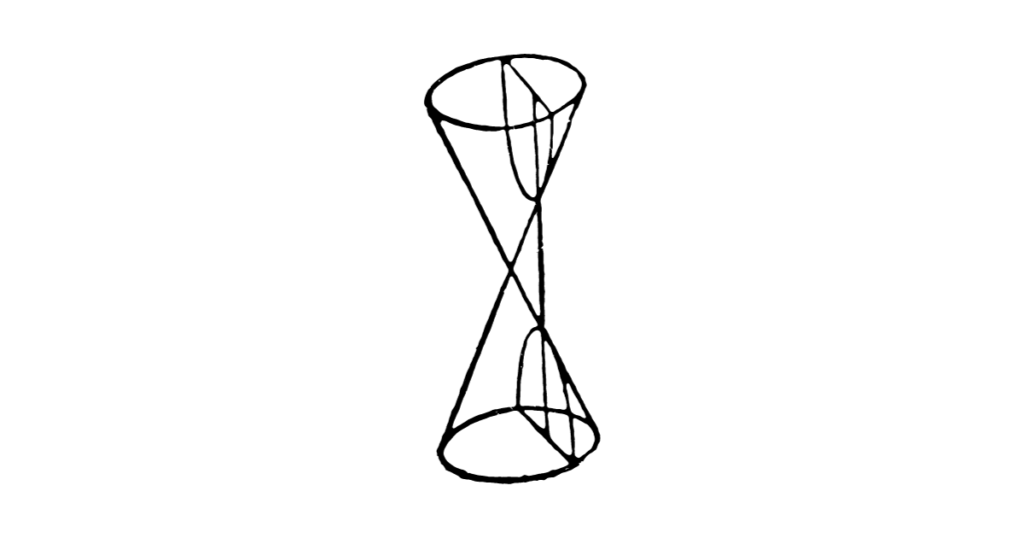
この「円錐曲線」とは、円錐の側面をさまざまな角度で切ることで、円、楕円、放物線、双曲線など、断面に異なる図形が現れるというものです。
この「円錐曲線」の起源は非常に古く、なんと紀元前3世紀頃から始まり、ギリシャの数学者アポロニウスによって理論が体系化されたことで知られています。
同じ幾何学にもかかわらず、少し操作を変えるだけで異なる図形が顔をだす。
円錐曲線の不思議さや法則性に魅せられた数学者たちがこぞって、研究し続けていた、そんな分野でした。
パスカルはそのような古代数学者たちが積み重ねてきた理論を、さらに上の次元へ押し上げるような理論を提唱したのでした。
この研究は、かの偉大な哲学者・数学者のデカルトすらも「凄すぎる…」と嫉妬するレベルだったのです。
【業績2】パスカルの三角形
中学のころに展開という概念を学びますが、こんな公式見たことありませんか?
\((x+y)^{2}=x^{2}+2xy+y^{2}\)
ちなみに、3乗にするとより複雑になります。
\((x+y)^{3}=x^{3}+3x^{2}y+3xy^{2}+y^{3}\)
数学者はもっともっと考えたいと思う生き物です。
これを4乗、5乗、そして10乗…と続いていけばどうでしょうか?
もはや計算できなくね?という領域にまで数字が大きくなってしまいます。
そんな中、パスカルは独自の視点からこの法則性を見つけ出したのでした。
それが「パスカルの三角形」です。

パスカルは数学の1つの分野「二項定理」の係数が、三角形のような不思議な性質を持っていることを発見しました。
例えば、((x+y)^{2}=x^{2}+2xy+y^{2}\)の係数の並びは、1,2,1。
\((x+y)^{3}=x^{3}+3x^{2}y+3xy^{2}+y^{3}\)の係数の並びは1,3,3,1。
\((x+y)^{4}\)の係数の並びは1,4,6,4,1。
\((x+y)^{5}\)の係数は1,5,10,10,5,1
というふうに並んでいくというわけです。
数学界における、不思議な法則の1つなのですね。
パスカル、ついに天才の社交場へ!
息子の才能を確信した、父エチエンヌはパスカルをメルセンヌ・アカデミーという知識人が集まるサロンに連れて行きました。
ちなみに、メルセンヌアカデミーとは、数学者・物理学者、そして神学者として活躍したマラン・メルセンヌが開いたアカデミーで、学会には、デカルト、フェルマー、またガリレオも関わるなど、世界的有名な科学者が集う権威ある学会だったのです。
まさに選ばれし者のみが入れる場所へ足を踏み入れた16歳のパスカルは、いろんな知識人たちと交流を交わし、さらに業界を驚かす発見をしていくのでした。
【業績3】計算機の発明
パスカルは19歳の頃に「パスカリーヌ」という、実用的な計算機を発明しています。
彼の父エチエンヌは税務官として働いていたのですが、
膨大な帳簿の計算に追われており、日々疲れ果てていたといいます。
そんな父の姿を見たパスカルは、「この煩雑な計算を、機械でなんとかできないか?」と考え発明したのが、パスカリーヌという計算機なのです。
【業績4】確率論の発展
その当時、貴族たちの間では賭け事が流行っていたのですが、
ある日、パスカルのもとに、シュバリエ・ト・メレという人物から「途中で打ち切られた勝負の賞金を公平に分けるにはどうすればよいか?」という相談が舞い込んできました。
勝負が終わっていたならば、分配は楽なのですが、途中で打ち切られたというのが問題を難しくしていますね。
彼はこの問題を、数学の友人であるフェルマーに手紙で問いかけました。
フェルマーはすぐに興味を持ち、互いに手紙のやり取りを通じて、数学的なアイデアを出し合うようになったのです。
その結果、パスカルは「期待値」という概念を導入し、現在の「確率論」を発展させました。
これが、現代の確率や統計、保険、AI予測、経済モデルなど、さまざまな分野に応用される大理論の出発点となったのです。
※関連記事

【業績5】大気圧の証明
パスカルの活躍は、数学にとどまりません。
彼は物理学の分野でも大きな功績を残し、今日では「ヘクトパスカル(hPa)」という気圧の単位にその名が刻まれています。
当時のヨーロッパでは、古代ギリシャの哲学者アリストテレスの影響力が非常に強く、「自然は真空を嫌う(horror vacui)」という思想が支配的でした。
この考え方は中世を通じてキリスト教神学と結びつき、12世紀以降のスコラ哲学を通じて広く浸透していました。
そのため、
「真空は存在しない」
「空間が空っぽになると、自然がすぐに何かでそれを埋める」
といった考えが学問の常識とされていたのです。
しかし、17世紀に入り、これに挑戦する新たな実験が登場します。
それが、イタリアの物理学者エヴァンジェリスタ・トリチェリによる「トリチェリの真空実験」でした。
この実験では、水銀を満たしたガラス管を逆さに立てることで、管の上部に何も存在しない「空白の空間」が生じる現象が観察されました。
これはまさに「真空」の存在を示すものであり、長らく信じられてきたアリストテレスの自然観に一石を投じたのです。
パスカルはこのトリチェリの実験に強い関心を持ち、自らも検証を行います。
なんと彼は、フランスにある山・ピュイ・ド・ドームにおいて、標高の異なる地点で水銀柱の高さを測定する実験を実施しました。
この観測から、「水銀柱の高さは大気の重さ=気圧によって決まる」ことを突き止め、大気圧の存在を科学的に実証したのです。
この発見により、自然に対する理解は大きく前進し、「真空は存在する」「空気にも重さがある」という新しい自然観が生まれました。
これらの業績はすべて10〜20代の前半頃までに打ち立てたものであり、パスカルは科学者としての非凡な才能をいかんなく発揮していったのでした。
思想家への転身
若き天才として、数学・物理・発明など多方面で類まれな才能を発揮してきたパスカル。
しかし彼の人生は、ある出来事をきっかけに、大きく転換していくことになります。
その転機は、1651年──父・エチエンヌの死でした。
エチエンヌはパスカルにとって、単なる親というだけでなく、教育者であり、知的な伴走者であり、心の支えでもありました。
父を失ったことは、パスカルの内面に深い喪失感と虚無をもたらします。
さらに、もともと虚弱体質だったパスカルの持病もこの頃から悪化。
日常生活にも支障が出るようになり、杖を手放せないほどの状態だったといわれています。
そうした肉体的・精神的な限界を前にして、彼はそれまで信じてきた「理性」や「科学」だけでは乗り越えられない現実に直面したのかもしれません。
この苦難の時期、パスカルは次第に数学や科学の研究から距離を取り、またこれまで交流していた学者仲間たちとも疎遠になっていきました。
代わりに、彼の関心はより深い「人生の意味」や「人間存在の本質」へと向かっていくのです。
ちょうどこの頃、妹のジャクリーヌは「ジャンセニスム」というキリスト教の一派に心酔し、ポール・ロワイヤル修道院に入っていました。
ジャンセニスムは、人間の原罪と神の恩寵を重視する厳格な思想でした。
パスカルもまたこの修道院を訪れ、静謐な空間の中で自身の人生と信仰について深く思索を重ねるようになります。
病弱な身体に鞭打ちながら、20代後半のパスカルは、これまでの人生とはまったく異なる方向へと歩みを進めていきました。
興味深い逸話があります。
当時、親交のあった数学者フェルマーが「また語り合いたい」と手紙を送ったのですが、パスカルはこう返しています:
「数学は精神を鍛えるには最適の学問だと思います。しかし同時に、それがまったく無用であることも知っています。
私が今歩んでいる道は、そうした学問とは根本的に異なるものです。
もはや数学というものが存在していたことすら、忘れてしまいそうです。」
こうしてパスカルは、かつての科学の世界に背を向け、
理性と信仰、有限と無限、苦悩と救済といった、人間の根源に関わる問題と静かに向き合い始めたのでした。
パンセの出版
科学者として輝かしい功績を残し、
そして信仰者として静かに生き方を問い続けたパスカル。
その晩年、彼はある静かな決意のもと、思索に耽っていました。
「人は、どう生きるべきか」
「人間とは、何なのか」
──そんな根源的な問いに向き合いながら、彼は日々、自身の思いを断片的なメモとして書き残していきます。
しかし、それらのメモが彼自身の手で出版されることは、ついにありませんでした。
病が静かに、しかし確実にパスカルの身体を蝕んでいき、1662年8月。
彼は、わずか39歳という若さでこの世を去ったのです。
それから間もなく、残された思索のメモたちは、彼を敬愛する知人や信奉者たちの手によって丹念に整理され、
一冊の書物となって世に送り出されます。
その書こそが、今なお世界中の人々に読み継がれている名著──**『パンセ(Pensées)』**です。
特に「人間は考える葦(あし)である」というフレーズはあまりにも有名です。おそらく一度は聞いたことあるのではないでしょうか?
このパンセには、科学者としての厳密な道、信仰者としての繊細な道と、2度人生生きた一人の天才がたどり着いた、「人間とは何か」という問いが綴られていました。
人間はひとくきの葦(あし)にすぎない。自然のなかで最も弱いものである。だが、それは考える葦 である。彼をおしつぶすために、宇宙全体が武装するには及ばない。蒸気や一滴の水でも彼を殺すのに 十分である。だが、たとい宇宙が彼をおしつぶしても、人間は彼を殺すものよりも尊いだろう。なぜなら、 彼は自分が死ぬことと、宇宙の自分に対する優勢とを知っているからである。宇宙は何も知らない。
だから、われわれの尊厳のすべては、考えることのなかにある。われわれはそこから立ち上がらなければ ならないのであって、われわれが満たすことのできない空間や時間からではない。だから、よく考えることを 努めよう。ここに道徳の原理がある。
すなわち、人間は宇宙のスケールから見れば取るに足らない存在。
でも、それを“理解できる”という一点において、宇宙よりも尊いということです。
パンセの思想は、科学と信仰、理性と感情、その狭間でもがき続けたパスカルの、魂の叫びだったのかもしれません。
パスカルまとめ
今回は、数学界の神童とよばれた天才パスカルの生涯を解説しました。
父親に数学を禁止されても数学をやったり、三角形の内角の和が180°であることを示したり、気圧の原理や思想書など、いろんな業種でさまざまな貢献を果たし、最後はとても深い人生への問いを残しています。
なぜ、そんな業績が残せたのか。
もちろん天才だから成せる業もありますが、それ以上に虚弱体質で苦しむ中で、常に考え抜いたパスカルの精神性がそのような結論を導き出せたのではないかと感じます。
パスカルが発見した、円錐曲線定理やパスカルの三角形、パスカルの原理など興味があれば、ぜひ調べてみてください。
きっと面白いですよ。











