どうも、マルタです。
多くの数学者は長い世代に渡って、円周率の研究をしてきました。
その研究ぶりは、もはや熱中通り越して、熱狂に近いです。
ちなみに、2019年の3月14日(円周率の日)に、米Googleの社員である岩尾さんは円周率を約31兆4000億桁まで計算し、ギネス世界記録に認定されました。
 マルタ
マルタもはや桁デカすぎて訳わかんねぇw
それほどまでに人々を熱中させる「円周率」とは一体どんな数字なのでしょうか。
今回は、円周率について解説していきます。
円周率とは?
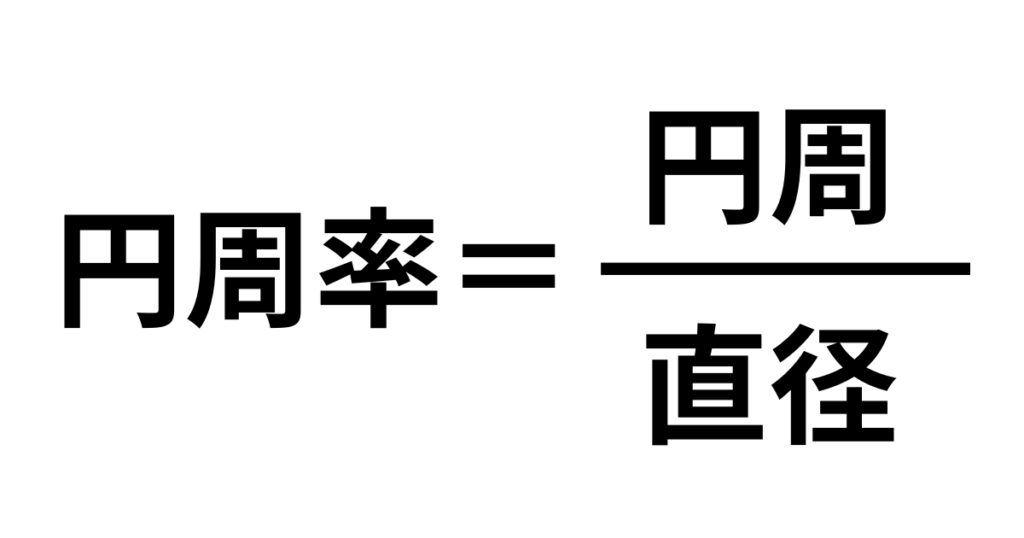
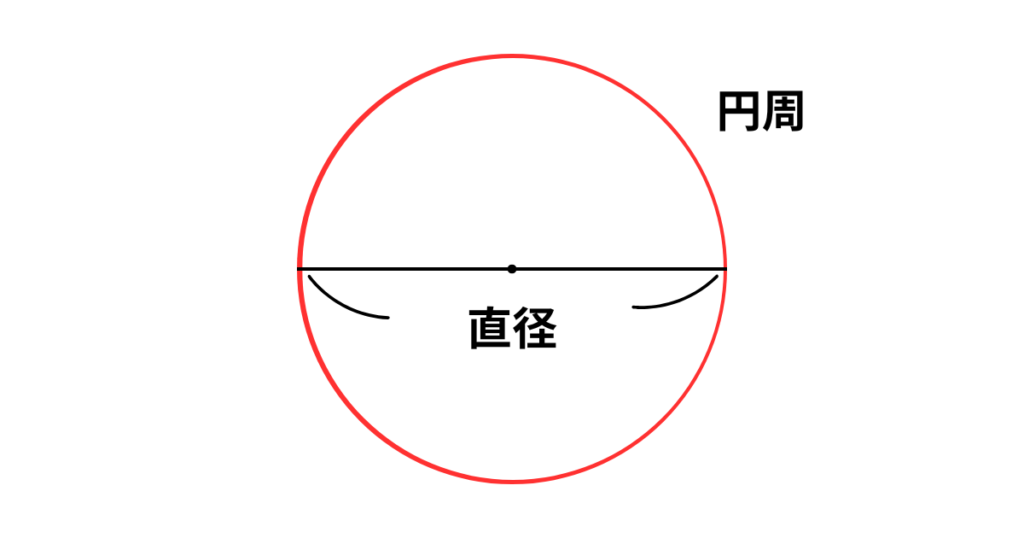
円周率とは、「円周÷直径」から導き出される3.141592…(小数点以降、数字が無限に続く)数字です。
一般的には記号で「π(パイ)」で表されます。


この円周率は、紀元前からすでに発明されており、紀元前2700年頃にピラミッドが建設された時に使われていたと言われています。
紀元前から誕生した円周率は、現代に至るまで数学者の関心を惹きつけてやまない数字として有名です。
そんな円周率は具体的にどのような経緯で発明されたのか?
円周率の歴史について解説していきます
円周率の誕生
昔の人々は、神殿や住まいの建設、他にもさまざまな便利な道具を作ることを営みとしていました。
その中でも、とりわけ重要だったのが「円」です。
あまりイメージつかないと思うのですが、実は昔の人々にとって「円」とは、実用性、美術性において非常に重要な意味を持っていました。
円がどのように人々の生活に影響していたのか、いくつがご紹介します。
農園の収穫量・土地価格の算出に円周率が活躍


はるか昔は、農業が中心の経済でした。
なので農地の大きさや面積で作物の収穫量を図っていたのです。
そんな農地ですが、四角や直線であれば、計算は簡単ですよね。
ですが、中には曲線や円形の農園があったため、どのようにして面積を求めるべきか?が議論になりました。
この議論の末、円周率という概念が登場しました。
貿易が盛んに行われるようになった円の応用


隣の国や都市との交易が始まった当初は、物資を運んでいました。
しかし、まぁ大変ですよね。
イメージするなら、食料を手いっぱい持って運ぶようなものです。
当然、現代のように車はありません。
かといって、物を手に持って運び続けるのは労力がかかります。
「さてどうするか…」と知恵を出し合った結果、発明されたのが「車輪」です。
そして、その時にも円周率が使われたのですね。
精密な設計技術に円が大活躍


昔の人々は建物を建てたりする時、幾何学の知識を活用していました。
幾何学とはザックリ言えば、図形に関する学問で、「三角形」や「四角形」、「体積」などを求める学問だとイメージしていただけたらと思います。
中学で学ぶ図形問題は、実は紀元前の頃から研究されていたのですが、これらの知識は神殿や大きな建物を作る際にも応用されていたのですね。
さて、紀元前は定規はありません。
じゃあどうやって、きれいな三角形や四角形を描くのか?
そこで活躍したのが、「円」でした。
例えば、三角形を描きたい場合。
2つの円の中心と、2つの円の交点を結ぶことで、定規を三角形が描けます。


円をうまく活用すれば、定規や分度器を使わなくても、正三角形は描ける!


角度を分割することもできます。


正確な線や図形を描くためには、正確な円を描くことが大事です。
なので、建築の一貫として、正確な円を描く必要があったのですね。
天文学でも円の知識が応用される


人類は昔から、1日の周期を図ることを試みていました。
- いつ明るくなるのか?暗くなるのか?
- 作物の収穫時期はいつか?
- 川の氾濫時期を予測して、浸水を予防する
このような時期を知るためにも、天文学は非常に重要な役割を持っていたわけですね。
当時の天文学者は天体の動きが円形に動いていることに気づき、天文学の研究と同時に、円の研究も進んでいったと言われています。
究極のシンメトリー!美の象徴としての「円」


円はアートや芸術においても非常に重要な役割を持っていました。
「美しさとは何か?」と考えた時、色んな要素はありますが、その中でも美しさを生み出す重要な要素が「左右対称性(シンメトリー)」です。
特にモニュメントや歴史の美しいと言われる建造物の特徴は左右対称であることです。
例えば、ピラミッド。


1648年に建てられたインドのタージマハル


日本だと東京タワー


リンカーン大聖堂


ミャンマーのシュエダゴンパゴダという仏塔


などなど。
世界の美しい建造物のほとんどが左右対称であることが特徴的です。
そんな左右対称性を持つ形の中でも究極的なのが「円」なのです。


なぜなら、円は回転させても左右対称であり続けるからです。
もっと言えば、球体はどんな向きに回しても永遠に同じ形を保つことができます。
このような美しさから、古代では円は美の象徴として考えられていたと言われています。
アルキメデスにより円周率は本格的に研究され始める


このように円周率にまつわる数多くの歴史があるのですが、実はまだまだ難点もありました。
それは、「円周率はとりあえず3でいっかー」という認識が強かったことです。
円周率は正確には3.14…ですが、当時の人々は「とりあえず3で」というノリでした笑
とは言え、それは仕方がないことで正確な求め方がわからなかったのが原因です。
本当は正確に測りたいけど、測れないから円周率は3だと考えられていました。
そんな中、「円周率はこうやって求められるぞー!」と声をあげたのがアルキメデスです。
彼は、天才と数えられる数学者の1人で、てこの原理や浮力を発見した功績があります。
そんなアルキメデスは、ついにみんなが望んでいた円周率の正確な値の算出に成功するのでした。
アルキメデス式円周率を求め方
アルキメデスの円周率を求める方法は非常に斬新です。
そもそもなぜ、円周率を求めるのが難しいのか?
それは曲線を含むからです。


それであれば、「直線にしてしまえば近い値は求められるぞ!」というのがアルキメデスの主張です。
「はぁ?」と思うかもですが、具体的にはこんな感じです。


円の外側と内側に図形を置き、それら図形の外周の和を求めることで、円周率の範囲を決定できます。
さらに、上の図では正六角形ですが、これを正十二角形、正二十四角形、正四十八角形、正九十六角形と増やすことで、周の長さを円に限りなく近づけることができます。
ちなみに、このような方法を「取りつくし法」と言います。
取り尽くし法(とりつくしほう、英: method of exhaustion、羅: methodus exaustionibus)は、与えられた図形の面積や体積を求める手法の1つで、その図形に内接する一連の多角形を描き、それらの面積を元の図形に収束させる方法である。積尽法、搾出法ともいう。また古代人の方法(仏: méthode des anciens)とも呼ばれる。
引用元:Wikipedia
正十二角形


正二十四角形


それを直径で割れば、より正確な円周率を求めることができるという方法です。
【考察】なぜ今なお円周率は研究され続けているのか?
不思議だと思いませんか?
円周率は紀元前にはすでに見つけられており、3.14…以降は無限に小数点が続くこともわかっている。
ぶっちゃけ、3.1415…以降はどれだけ桁数が増えようが、ほぼ誤差ですよね(←オイw)
発見された桁数を増やしたところで、「実用性あまりないよね?」と感じるのが正直なところではないでしょうか。
それでもなお、現在も更なる円周率の桁数を求める研究は続いているわけです。
では、なぜ今なお円周率は研究され続けているのか?
考察していきたいと思います
【考察1】円周率の新しい導き方を発見するため
実は円周率の求め方は、今回の方法だけではありません。
なんと全部で20種類以上存在します。
昔は、手書きでしたが現在はパソコンを使って色んな求め方がされています。
ちなみに、インドの数学者ラマヌジャンは円周率を求める公式の1つとして、以下の公式を発見しています。


このように円周率を求める方法は数多く存在し、また発想を変えることで新しい手法を生み出すこともできるのですね。
新しいアイデア発見の一環として円周率の研究がされ続けているのではないかと思います。
【考察2】無限の果てを求めて


これはシンプルにロマンの追求です。
現在、円周率は無限に続くことが証明されていますが、「もしかしたら、終わりがあるかもしれない」、「無限の果てがあるかもしれない」という思いがあるのかもしれません。
あるいは、無限に続くとしても、法則性が見つかるかもしれない。
そんな期待や願いがあるかもしれません。
もし円周率に法則性や終わりが見つかれば、それだけで人類の大きな進歩につながる可能性もありますからね。
まとめ
今回は円周率について解説しました。
円周率は、実社会において役立つ活用から始まりました。
2000年以上も研究され続け、そしてこれからも研究は続くのです。
円周率の桁数を覚えるのはシンドイですが笑、円周率を求めてこれまでの歴史がどのような道を辿ってきたのか、思いを巡らせてみると面白いですね。











