どうも、マルタです。
三角関数は逆関数や双曲線含めるとかなりの公式がありますよね。
油断すると混乱してしまうので、sinの三角関数やarcsinの逆関数、双曲線についての公式をまとめます。
ぜひブックマークして、いつでも見直せるようにしておいてください。
三角関数 sin.cos.tanの公式
三角関数とはsinθ,cosθ,tanθの関数です。
※以降、θをxと表記し、xの定義域は0≦x≦2πとします。
三角関数の公式
三角関数に関する代表的な公式をご紹介します。

三角関数の変換の式

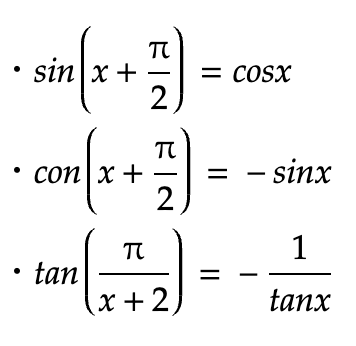

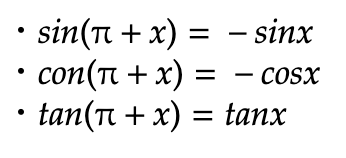
三角関数の加法定理

三角関数の2倍角の公式
三角関数の2倍角の公式です。

この公式は暗記ではなく、加法定理のβをαに変えることで求まります。
三角関数の3倍角の公式
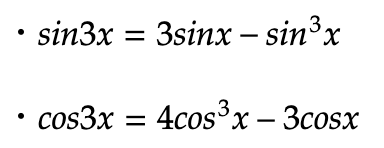
これらの公式も2倍角を求める手順と同じで、加法定理のαを2α、βをαに書き換えることにより求まります。
ただし、計算が少し煩雑なので3倍角は覚えるのが一番楽です。
万が一忘れた場合に、加法定理から導くのがオススメです。
三角関数の半角の公式

こちらは三角関数の分野だけでなく、微分積分でもよく使われます。
微分
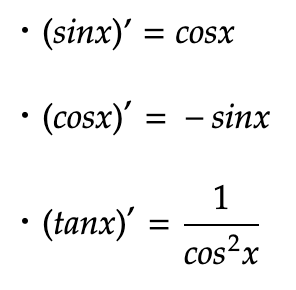
積分
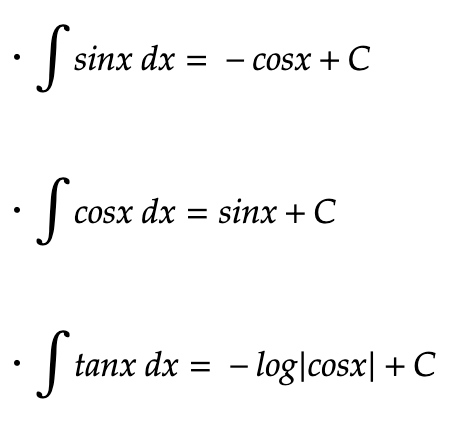
※Cは積分定数
逆三角関数の公式
逆三角関数はいろんな表記方法がありますが、ここではarcsin、arccos、arctanと表記します。

逆三角関数とは…
逆三角関数とは、

あるいは、

と表記される関数のことです。
注意しなければならないのが、これは三角関数の逆数ではない。つまりsin、cos、tanとは全く別だということです。
ですので、逆数の表記との混乱を避けるため、sin、cos、tanの頭に「arc」が付くケースもあります。
また逆三角関数が存在するための条件は以下の通りです。
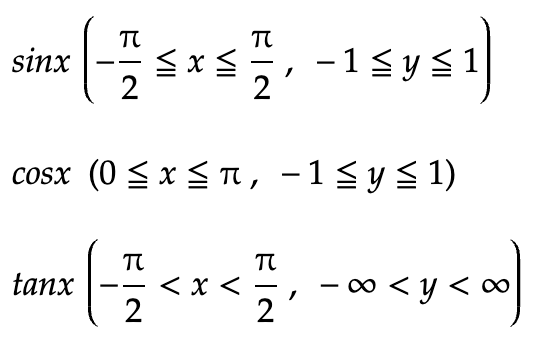
逆三角関数の微分
逆三角関数の微分は以下の通りです。
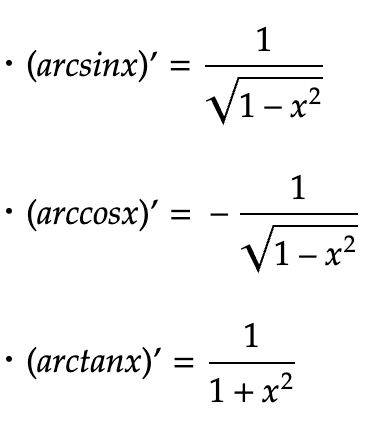
双曲線(ハイパボリック)の公式
双曲線関数の公式は以下の通りです。
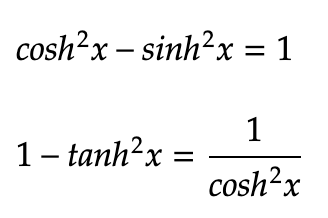
sin、cos、tanの公式に似ているのが特徴です。
双曲線関数(ハイパボリック)とは
双曲線関数(ハイパボリック)とは、工学系で主に使われる関数です。性質や公式は三角関数に似ています。
ハイパボリックはsin、cos、tanにh(ハイパボリック)を付け加えて
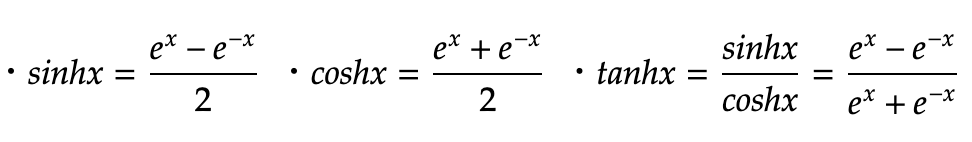
このように表記します。
※eはネイピア数
双曲線(ハイパボリック)の加法定理

双曲線関数の加法定理もsin、cos、tanの加法定理に似ているのが特徴です。
双曲線(ハイパボリック)の2倍角の公式
双曲線関数の2倍角の公式は以下の通りです。
双曲線関数の加法定理のβをαに書き換えることで、導き出すことが可能です。
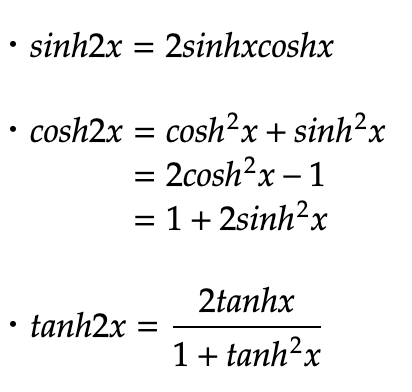
双曲線(ハイパボリック)の微分
双曲線関数の微分は以下の通りです。
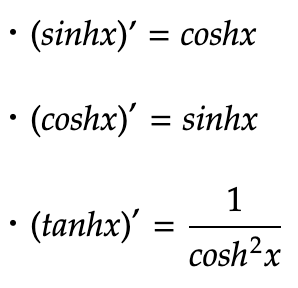
双曲線(ハイパボリック)の積分
双曲線関数の積分は以下の通りです。
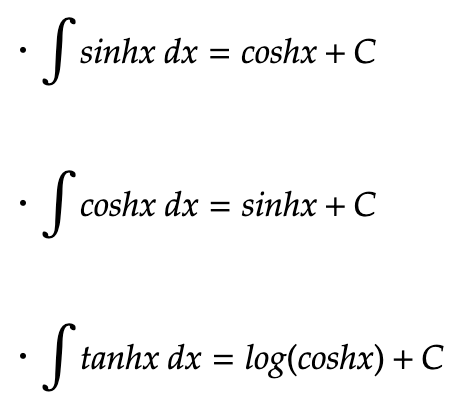
【補足1】双曲線関数(ハイパボリック)の逆関数
双曲線関数の逆関数は以下の通りです。
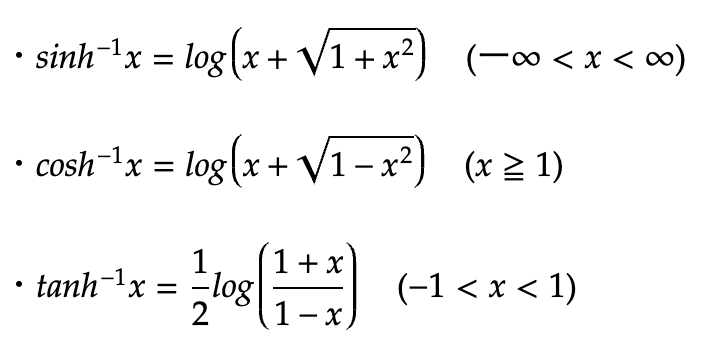
【補足2】secant、cosecant、cotangentについて
secant(セカント)、cosecant(コセカント)、cotangent(コタンジェント)の代表的な公式は以下の通りです。
secant(セカント)、cosecant(コセカント)、cotangent(コタンジェント)とは…
secant(セカント)、cosecant(コセカント)、cotangent(コタンジェント)とは、sin、cos、tanの逆数です。
secantはsec、cosecantはcot、cotangentはcotと表記されます。
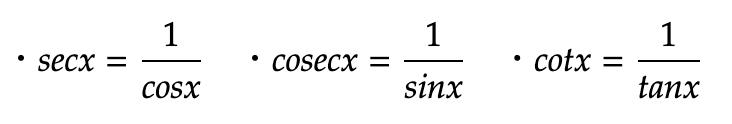
とはいえ、普段はあまりsec、cosec、cotは使われません。
普通に分数で表示する方がわかりやすいからです。
とはいえ、書籍によってはたまに記載されているケースもあるので、知識として身につけておいて損はありません。