どうも、丸田です。
今回は非常に面白い動画を教えてもらったので共有します。
それが「Animation vs. Math」
このアニメーション、非常にクリエイティブに富んでおりまして。
数学を知っている人はもちろん、数学を知らない人も思わず「すげぇ!!」と唸ること間違いなしです。
今回はこの動画の考察と詳細の解説をして参ります。
なお、ネタバレ含むのでもしよければ動画視聴後に読み進めていただけたらと思います。
物語の構成と舞台設定
物語の構成
この動画の物語の構成としては、「人類が数学を発見して、虚数を見つけ、最も美しいといわれる「\(e^{iπ}=-1\)」を発見した歴史を端的にまとめたものなのかなぁと感じました。
舞台設定
暗闇の空間に放り込まれた人間が困惑している場面からスタートします。
この暗闇空間はおそらく実数の世界だと思われます。
一方、真っ白な世界はパラレルワールドの虚数の世界だと思われます。(後半で登場する)
最初は主人公がいろいろ数字を使ってなんやかんや行いますが、おそらく実数の世界を把握するための試行錯誤だと思います。
「=」や足し算、引き算、割り算など…。
まるで昔の人々があれこれ試していたようなそんな行為を行っているわけですね。
その中で突如現れたのが、「\(e^{iπ}=-1\)」。
数学の中でも最も美しい公式と呼ばれているからです。
なぜ「\(e^{iπ}=-1\)」が実数の世界に存在するのか?
それは虚数を含みながら答えが実数になる性質があるからだと考察されます。
ポケモンで例えれば、伝説のポケモン「ミュウ」みたいな存在かなと。
なので、実数の人間は捕まえようします。
しかし\(e^{iπ}=-1\)は虚数空間へ逃げるわけです。
※動画の中では、「e^iπ」は自身に「i(虚数単位)」をかけることで、虚数空間へ移動していることから「i」が実数と虚数の世界をつなぐ鍵かと思われる。
さぁ果たして、人間は無事「「e^iπ」を捕まえることができるのでしょうか?!という話かなと思われます。
動画内の小ネタ説明
ここからは動画の小ネタをご紹介していきます。
2:49:割り算のバグ発生
6÷0を実行すると無限に動作が起こるのは、0で割る行為が数学の理論に反するので、そのバグを表しているのか?と思われます。
3:09:2乗で面積
これは(6+2)の2乗は縦横8の面積を表していると思われます。
3:16:3乗で体積
これは縦横奥行き4の立方体を表していると思います。
3:18:4乗で四次元
これはすべてが4の四次元の立体を表していると思われます。
3:21:5乗で五次元
これはすべてが4の五次元の立体を表していると思われます。
4:12:「\(i^{2}=-1\)」
なぜ「\(e^{iπ}=-1\)」は扉をくぐり抜けても逃げられなかったのか?
→「\(e^{iπ}=-1\)」は自ら「i」を用意することで虚数になれるので、虚数の世界へいけます。
しかし、人間が投げた「i」があたり「(i^{2}=-1)」になってしまったことで実数に変化したことで虚数の世界へは逃げられなかったと考えられます。
4:17:オイラーの公式
e^iπ=cos(pi)+isin(pi)という
オイラーの公式です。
4:22:謎のジャンプ
このジャンピングは不明です笑
4:56:\(\frac{π}{4}\)回転
角度が\(\frac{π}{4}\)だけ変化したため\(e^{iπ}\)が上部に移動しています。
またその際の\(e^{\frac{π}{4}}\)の値は\(\frac{1}{2}+\frac{1}{2}i\)であるため、画面の中途半端な位置にいるのかなと思います。
※主人公はそこへは行けないと思われる。
5:18:複素数平面
虚数(=複素数)を表す平面座標を表現しています。
6:00:弧度法
半径1の円(単位円)を考え、ある弧の長さ(例えばθという長さ)に対する中心角をθと定義する。
そして、この角度はrad(ラジアン)という単位で表す。
このとき、半径r、中心角θradに対する弧の長さはrθとなります。
これを弧度法と呼び、そのことが解説されております。
ちなみに半円までの角度はπです。
6:50:sinθのグラフ
sinθの波形グラフです。
6:55:cosθのグラフ
cosθのグラフの波形です。
7:34:オイラーの公式の別記法
「(i^{2}=-1)」は別の表記も可能です。動画内だと、
\(e^{iπ}=\displaystyle\sum_{n=0}^{∞}\frac{(iπ)^{n}}{n!}\)
と表記されていました。
その後、発射される弾の数字が変わるのは、n=1,2,3,,,と弾の順番にnが1ずつ増えているので、その影響で数字が変わっている(ちなみに、弾の数は無限大にあるので、永遠と打てる仕様っぽい)
7:45:面積シールド
シールドを貼っているのは、4という数字と長さ1の棒(のようなもの)、そして円周率πを組み合わせることで、4πとなり半径1、4×πの面積となるためその面積がシールドとなっている。
7:50:円柱の体積
どこかで拾った8をかけることで、半径1の底面積と横幅8の円柱になって反撃している。
なお8πr^2は円柱の体積(と思われる)
8:05:グラフ反転
自分にマイナスをかけることで、グラフ上の位置が反転してことなきを得ている。
8:25:ハイパボリック
ハイパボリックsin、ハイパボリックcosという公式。
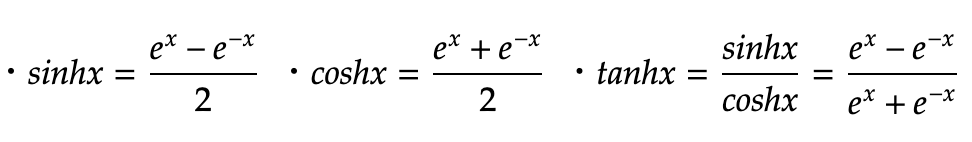
とにかくすごそうなsin,cosぐらいのイメージでOKです笑
主に工学系で使う数式です。
※動画内ではtanhxは出ておりませんが、おまけとして。
8:32:tanθ
sinθ/cosθ=tanθです。
ここでは、f(x)=9tanθとなりました。
9:02:半回転
πを横向きの直線にかけることで、直線がπ(半円)だけ回転。
その直線につかまることで、主人公は移動しています。
9:26:無限大
「∞」を奪うことで相手の弾がなくなり、主人公の武器の弾が無限大に増えています。
これで形勢逆転ですね。
ちなみに9:30あたりで、放った弾が不思議な形をしておりますが、これはtanθのグラフの形をしております。
9:40:ベクトル空間
Span ({x1,x2,x3,x4})とありますが、これはベクトル空間を意味しています。
ですが、あまり気にしなくて良いと思われます。
9:58:積分
limは極限を表しており、シグマと極限を組み合わせることで積分(∫)となります。
その∫の記号が相手の武器に変化しています。
10:18:平行移動
グラフに「i」を足すごとに上に平行移動しております。
11:25:虚数空間
虚数の世界へ突入です。
√-1などがあることから確定で間違い無いでしょう。
11:50:実数の世界へ
「i」をかけることで、実数の世界へ戻っています。
13:04:ガンマ関数
ガンマ関数です。
13:04 n次元球面
ガンマ関数を使ってn次元球面を作成しております。
最後は別の次元へ主人公が飛ばされてしまいましたね。
これは人類がさらに深淵な数学の世界へ向かうという暗示なのでしょうか。
13:47
最後はオイラーの公式でよく使われる、ζ(ゼータ)、Φ(ファイ)、δ(デルタ)が登場します。
そして、最後には背景にうっすらℵ(アレフ)が存在しています。
ℵは無限大に大きな数を表現する記号。
数字は更なる無限大への続く余韻を残して終わっています。
以上で考察終わりです。









