どうも、丸田です。
数学といえば、方程式。方程式といえば、数学。
とは限らず。
数学以外の分野でも使われる言葉ですよね。
- 成功の方程式
- 幸せの方程式
- 恋愛の方程式
- 運の方程式
などなど。
なんなら、僕マルタの名前を使って、「マルタの方程式」という言葉も瞬時に作れちゃいます。
それくらい汎用性高い「方程式」という概念。
ではなぜ、方程式というアイデアは生まれたのでしょうか?
そしてなぜ、古代の人々は方程式を解こうとしてきたのでしょうか。
今回は方程式の歴史を解説しながら、方程式の考察を綴って参ります。
※考察なので、厳密さに欠けますが、1つのロマンとして見ていただけると幸いです。
なぜ人は方程式を解くのか?
ずばり「真理を解明したいから」ではないでしょうか。

日常のワンシーンを想像してみてください。
本屋に置いてある「幸せの方程式(仮)」の本を買う人の胸の中は、「幸せになる答えがわかるかも!」という期待感に溢れていると思うのです。
方程式には、真理を秘めた魅力がありますからね。
これは数学者も同じです。
数式を解けば何か真理の一つがわかるかもしれない、そんな期待があるのです。
なので、方程式を解きたいと思う気持ちは、答えがわかるかもしれないからという期待から来るものだと思っています。
ちなみに、方程式の研究は紀元前2300年頃には、メソポタミア、パビロニア地域にて、すでに始まっていました。

紀元前2300年ですよ!
こんな昔から方程式の問題があったなんてビビりますよね。
当時は現代のような紙はなく、その代わりに粘土板を使っていたそうです。
「世の中の真理を知りたい!」とはいえ、いきなり全てを知ることはできません。
だからこそ、身近な事例からスタートしていきました。
まずは建物の面積や高さなど、周囲の現象を式にしていき、その法則を解き明かしていけば、真理がわかるのではないか、
という具体→抽象のステップで真理への追求を進めていったわけですね。(具体→抽象を帰納法と言います)
その法則を解き明かすために、生まれた1つのアイデアが方程式です。
この方程式の解が見つかれば、真理が一つわかる。
その研究は紀元前から始まり、そして現代に至るまで続いているのです。
一次方程式、二次方程式の研究の歴史

一次方程式(直線)、二次方程式(曲線)は紀元前から研究されていました。
その中でも、二次方程式は西暦600年頃にめざましい発展を遂げます。
舞台はエジプトやバビロニア、インド。
当時のメインテーマは、二次方程式でした。
この二次方程式はさまざまな解決方法が編み出されるなど、非常に盛んだったのですね。
ちなみに、この当時から二次方程式の解の公式は発見されていました。
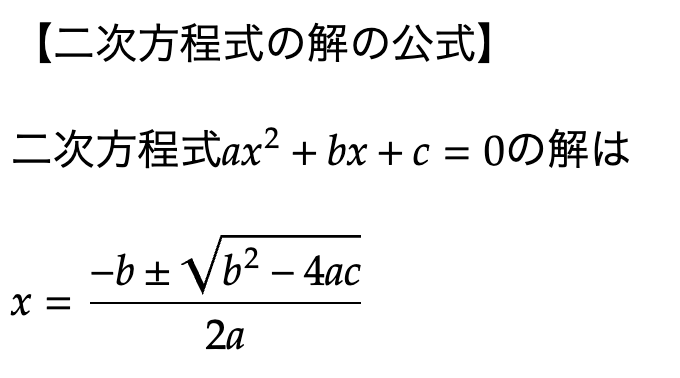
そんな彼らにも悩みがありました。
それは「解がない」という現象が起こるということです。
「解を求めたい!真実を知りたい!」と願う人からすれば、「解がない」というのは非常に困りますよね。
しかし打開策はなく「この方程式は解けない!仕方がない!」と諦めていたそうです。
ではなぜ解がない、という状況が起こるのか?
それは負の数(0より小さい数字)が出現したからです。
そう!現代においてはマイナスの数は当たり前。
マイナスの数字も珍しくありません。(氷点下など)
しかし、マイナスの概念がない当時の時代は、マイナスの解が出たら「解なし」と判断されていたのです。

ですが、方程式に答えがないというのは放っておけないですよね。
そこで0より小さい数字を認めようという考えが徐々に広まりました。
※地域差はありますが、その後0は数字として徐々に世界各国に浸透していくこととなります。
0とマイナスの概念を取り入れることで、一気に方程式は発展したのでした。
0、負の数に関する記事はこちらでも解説しているので、ぜひ参考にしてみてください。
すごいけど実はめっちゃ苦労人!?数字「0」の誕生と歴史について
負の数の歴史から見えるインドとヨーロッパ数学観について
中世イタリアで3次方程式が発展する
二次方程式の研究が進んでから、1000年後。
舞台は16世紀、ルネサンス期のイタリア。

この時代に誕生したのが三次方程式です。
当時のヨーロッパでは方程式の難問を出し合って解き合うという、数学の知力を競い合う競技が盛んでした。
頭の良さがお金、そして名誉が手に入るという数学者にとって黄金時代ではないでしょうか。
そんな中、難問なのが三次方程式だったのです。
二次方程式はすでに解の公式が存在するので、計算すれば誰でも答えを導けます。
しかし、三次方程式には解の公式が存在せず、もっといえば、この当時にも「解が存在しない」という現象が起こっていました。
二次方程式、三次方程式と解がないという状況をどうにかできないもんか!
その悩みを一撃で解消する素晴らしい発明がなされました。
それが「虚数」なのです。
虚数とは「2乗すると−1」という変わった数ですね。
世間からは、存在するかしないか不明、信じるか信じないかはアナタ次第な都市伝説扱いされる虚数。
しかし、実は「方程式の解がない」という数千年にも渡る問題を解決した、とても偉大な数なのです。
もちろん、虚数が受け入れられるには非常に時間がかかりました。
というのも、長年マイナスとマイナスをかけたらプラスになると考えられていたからです。
もしマイナスとマイナスをかけてもマイナスという概念を取り入れた結果、今までの数学の築き上げてきた理論が崩壊したら…?
そんな不安が数学者の中に存在していました。
しかし、中には大胆にも虚数を取り入れようとする人もいたそうです。
「まぁとりあえずやってみたらいいやろーほれー」「ば、ばかやろーーーーーー!!」
きっとこんなイメージです笑
しかし、実際に虚数を導入してみても、数学の論理体系には影響を与えず。
むしろ虚数自体が、今までの数学理論に馴染んでいく!
こうして数字の概念が拡張された新たな数学をこぞって数学者が研究するようになったのです。
ちなみに、「虚数」と名付けたのはかの有名な哲学者ルネデカルトでした。

ルネデカルトは「2乗してー1だと!?そんな数字は存在しねーよ!だが、、、まぁ一応名前ぐらいはくれてやる…」という皮肉をこめて「虚数」と名付けました。
しかし、その予想を反して、さまざまな虚数の性質が明らかにされていきました。
その中でも有名なのが、ドイツの数学者ガウスでした。

彼はなんと虚数を平面座標に落とし込む手法を提唱したのでした。
これをガウス平面と呼ばれます。

以降、このガウスの手法は現代にも活用されております。
この発見からガウスは「虚数は存在する。だからちゃんと名前つけてやろうぜ」ということで「複素数」と名付けたのです。
※虚数は一般的には、複素数と呼ばれます。
さらに虚数(=複素数)の誕生により、n次方程式は複素数の範囲で必ず解を持つということが証明されました。
「方程式に解がないをなんとかしたい!」という長年の夢が実現したのです。
そしてついに、三次方程式の解の公式も発見されるのでした。
三次方程式の解と四次方程式の発展
三次方程式の解の公式はタルタリアという数学者が発見しました。
その三次方程式の解の公式を広めたのは、カルダノです。
タルタリアが発見して、それをカルダノが広める。
あぁ…なんて素晴らしいコンビなんだ!仲良いんだなぁ、、、と思ったアナタ!
残念ながらそんな美しいドラマはありません笑
カルダノは「絶対に解の公式は口外するな」というタルタリアとの約束を破って、三次方程式の解の公式を自分の本の中で公表してしまうのです笑
なんつー無礼者!
時を遡ります。
三次方程式の解の公式を見つけたタルタリアの元に、カルダノが訪れます。
ちなみに、タルタリアはこの発見を誰にも打ち明けていないことから、おそらくカルダノは謎の嗅覚で公式の匂いを嗅ぎつけたのでしょう。
カルダノはタルタリアに必死でお願いします。
「頼む!三次方程式の解の公式を教えてくれ!」「だめだ!」
タルタリアは毅然とした態度で断ります。
しかし、しつこくお願いしまくるカルダノ。仕方ないとタルタリアはカルダノを信じて公式の存在をしゃべったのでした。
そして、タルタリアとカルダノは固く約束を結びます。
「いいかカルダノ。この公式は絶対に口外するなよ。」「わかったよ!何があっても絶対に言わねぇ!これは男と男の約束だ!」。
後日カルダノは、自身の著書に公式の存在を書いて出版したのでした…。
「コノヤロー!!」
もちろん激怒したタルタリアはカルダノに数学の決闘を挑みます。
しかし、カルダノはなんやかんや理由をつけて、弟子のフェラーリに決闘の代役を勤めてもらいました。
「ふん、まさか弟子を出すとは。カルダノも腕が落ちたもんよのぉ…。いざ勝負!!」
その結果、タルタリアは敗北。。。フェラーリの勝利となりました。
しかし、タルタリアは決して手を抜いていたわけではありません。
カルダノ側には三次方程式の解の公式を知られてしまっていました。
そこでタルタリアはとっておきの必殺技を繰り出したのでした。
それが四次方程式。
四次方程式は今までの方程式とは一味も二味も違い、更なる難易度を誇る問題です。
しかし、カルダノの弟子フェラーリはなんとその超難問である四次方程式を解いてしまったのでした。
「バカな!なぜ解けた!?」理由はシンプル。
フェラーリはなんと秘密裏に四次方程式の解の公式を発見していたのでした。
タルタリアの攻撃「四次方程式!」とんでもない攻撃が繰り出されたぁ!!どうするフェラーリ!?
なななななんとぉ!!フェラーリが「四次方程式の解の公式」でカウンター!
フェラーリ「無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄無駄ァーーー!!」
これはクリティカルヒットかぁ!?
ああぁぁーーーー!!タルタリアダウン!タルタリアダウン!タルタリアがリングに沈んだぁぁぁ!
勝者フェラーリィィィィィイ!!!
ここにイタリアから新チャンピオンが誕生しました!!フェラーリィィィィイ!!
観衆:ウォォォォォォォォオォォォ!!
ってな具合に、返り討ちにされたタルタリア。
中世のイタリアにて、実にドロドロとした歴史があったわけです。
とはいえなんだかんだ、方程式は発展していったのでした。
タルタリアはグッジョブなのかどうかは不明ですが、こうして三次方程式と四次方程式の解の公式が見つかったわけです。
この調子で、次は五次方程式だー!六次方程式だー!と勢い付いていた数学業界。
しかし、そんな状況にも終焉が訪れます…。
打ち砕かれたロマン
きっと誰もが「これで方程式のすべてがわかるかもしれない!」と希望を抱いていたでしょう。
そこに彗星の如く現れたのが、ノルウェーの若き天才数学者アーベル。
彼の生涯は短いですが、「五次方程式だー!六次方程式だー!と勢い付いていた数学業界」を一気に黙らせる非常にインパクトある理論を提唱しました。
彼が残した証明は、簡単にいえば「五次以上の方程式は今までのような手法では解決することができない!」となりました。
わかりやすく言えば、5次方程式以上は、今までのように足したり引いたり、虚数を用いても解決できない。
言い換えれば、五次方程式を解決するには、今までとは全く違ったやり方を見つける必要がある、というわけです。
このインパクトは、もうえげつなくて。
タルタリアの三次方程式の解が刀、フェラーリの四次方程式が銃だとすれば、アーベルの理論はもはや隕石です。
さらに後に現れる若き天才数学者ガロアによって、アーベルの理論はさらに整備されます。
「五次以上の方程式において、解の公式が存在しない」ということを提唱しました。
今までの四次方程式までは、どんな方程式でも解の公式に当てはめることで必ず解を導くことができました。
しかし、五次以上は解ける方程式もあるし、解けない方程式もあるかもしれない、とにかく普遍的に解決できる手法ない!みたいな感じです。
ガウスの証明した「n次方程式には複素数の範囲で解が存在する」
アーベル・ガロアによって「解の公式は存在しない」
これは答えがあるのはわかっているのに、その方法はわからないことを意味します。
この理論によって、数学の方程式は非常にもどかしい思いをしたことでしょう。
イメージするなら、目の前に財宝があるのに、別の道からしか辿り着けないみたいな感じでしょうか。
こうして方程式への希望が崩れ去っていったのでした。
新たな方程式研究の幕開け
今現在において、5次以上の方程式を解決する普遍的な方法は見つかっておりません。
とはいえ、これは決して悲劇でもありません。
なぜなら、数学は困難を迎えると新たな学問が生まれるからです。
この時代に新たな「ガロア理論」と呼ばれる理論が誕生しました。
ガロア理論とは、ざっくり言えば「解がどのような性質を持つか」を探る理論です。
この理論により、代数方程式の解の性質を把握しやすくなるのですね。
※このあたりは、僕も勉強中なので、ここでは浅く取り上げる程度で終わります。
この学問によって、答えそのものを導くのではなく、答えの周辺から性質を明らかにする方向での研究が進んでいきます。
そして、研究はこれからも進んでいくのでした。
方程式の歴史 まとめ
今回は、なぜ人は方程式を解くのか?というテーマから、方程式の歴史をご紹介しました。
方程式の歴史も非常に面白いですよねぇ。
0、負の数、虚数の導入によって、研究が発展した歴史を振り返ると、新たな発見と方程式進化には密接な関係があるように思えます。
もっと抽象的にいえば、真理の追求には新たな発見や概念を認める柔軟さが必要なのかもしれません。
ぜひ今回の内容が参考になれば幸いです。