どうも、丸田です。
今回はフィボナッチ数列について解説していきます。
フィボナッチ数列という言葉自体はもしかしたら聞いたことがあるかもしれません。
では、フィボナッチ数列が具体的に何がすごいのか?解説していきます。
フィボナッチ数列とは簡単にいえば、自然法則を表した神秘の数の並びです。
とまぁ、なんのこっちゃ?って話だと思うので、より細かく解説していきます。
ただその前に、フィボナッチ数列の凄さを理解する前にまずは「黄金比」を知っておく必要があります。
ということで「黄金比」について解説していきます。
黄金比について
黄金比とは、美しいとされる比率であり、その比率は1:1.618…と表されます。


…は無限に数字が続きます
不思議なもので、太古の昔から人が自然と美しさを感じざるをえない比率でもあり、「神の比」とも呼ばれているそうです。
紀元前500年頃に活躍した数学者ピタゴラスも黄金比を研究していたとされています。
つまり「美しいな」とか「これいいな」と感じるものには、黄金比が隠れているケースが多いのです。
有名なものであれば、パルテノン神殿やモナリザの顔と縦と横の比は黄金比と言われています。


またレオナルド・ダヴィンチのスケッチ人体には大いに黄金比が活用されています。


さて黄金比について解説したところで、いよいよフィボナッチ数列をご紹介していきます。
フィボナッチ数列について
フィボナッチ数列とは、黄金比と関連した数字の並びです。
そもそも「数列」とは数字を並べたものですが、数字をどのような規則で並べるか、次第ではさまざまな規則性が生まれるものもあります。
例えば、「1,2,3,4,5,6,7,8,9,10,11…」
これは数字を1ずつ足して並べた数字の列になります。
あるいは、「1,2,4,8,16,32,64,128,256…」
これは1から始まり、2をかけていくことで並ぶ数字の列です。
このような規則性がある数字の列はいくらでも作ることができるわけですが、その中で最も美しいのが「フィボナッチ数列」なのです。
その中でも最も神秘的な規則を含むのがフィボナッチ数列なのですね。
フィボナッチ数列は黄金比と密接な関係があります。
フィボナッチの発見した数列は以下のとおりです。
「1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610」





規則なんてあるの?
と感じるかもしれませんが、これは「1つ目と2つ目の数が、1から始まり、1つ前の数と2つ前の数を足した数字が次の数字になる」という規則を持っています。
具体的に説明します。
フィボナッチ数列の初めの数は「1」です。
次の2つ目の数も「1」です。
- 3つ目の数は、1つ前の数字「1」と2つ前の数「1」を足した「2」となります。
- 4つ目の数は、その前の数「2」と2つ前の数「1」を足した「3」となります。
- 5つ目の数は、その前の数「3」と2つ前の数「2」を足した「5」となります。
- 6つ目の数は、その前の数「5」と2つ前の数「3」を足した「8」となります。
- 7つ目の数は、その前の数「8」とその前の数「5」を足した「13」となります。
- 8つ目の数は、その前の数「13」とその前の数「8」を足した「21」となります。
…といった具合に、永遠と数が増え続ける規則があるのですね。


いかがでしょうか。少しずつ規則性が見えてきたでしょうか?
ではこの数字の羅列の何がすごいのでしょうか?さらにフィボナッチ数列の神秘性に迫って参ります。
【特徴1】連続する2数を割った数値が黄金比に近づく
フィボナッチ数列の驚くべき性質に、連続する2数のうちの小さい数で大きい数を割ると、黄金比に近づくという性質があります。
例えば、
3と5は連続する2数です。このうち小さい数3で大きい数5を割ると、5/3=1.666666…
5と8は連続する2数です。このうち小さい数5で大きい数8を割ると、8/5=1.6
13と21は連続する2数です。このうち小さい数13で大きい数21を割ると、21/13=1.615384…
このフィボナッチが発案した数列は、連続する2数のうち、小さい数で大きい数を割ると、黄金比に近づくという不思議な性質があるのですね。
もっと大きな数で試してみましょう。
377と610はフィボナッチ数列の中で連続する2数です。このうち小さい377で大きい610を割ると、610/377=1.61803…
46368と75025はフィボナッチ数列の中で連続する2数です。このうち小さい46368で大きい75025を割ると、75025/46368=1.61803399…
というように、どんなに大きい連続する数を選んでも、小さい方の数字を割ると黄金比に近づくのです。
しかも値が大きければ大きいほど黄金比に正確に近づいていくのですから不思議ですよね。



ちなみに、46368はフィボナッチ数列の25番目、
75025はフィボナッチ数列26番目の数字です。
【特徴2】螺旋構造の数列
さらに不思議なのはフィボナッチ数列の数字法則は、なんと自然界にも見つけることができるのです。
そのためには、まずフィボナッチの螺旋について解説していきます。
まずフィボナッチ数列の最初と2番目の数は「1」です。
そこで1辺の長さが1の正方形を作ります。


次に同じ1辺の長さが1の正方形を並べます。
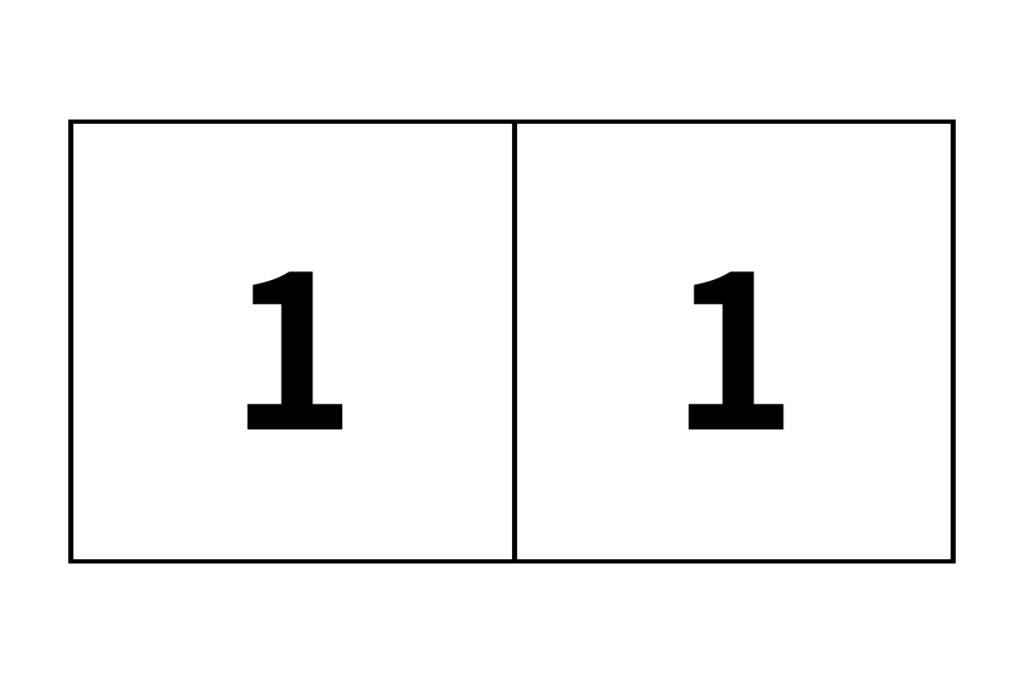

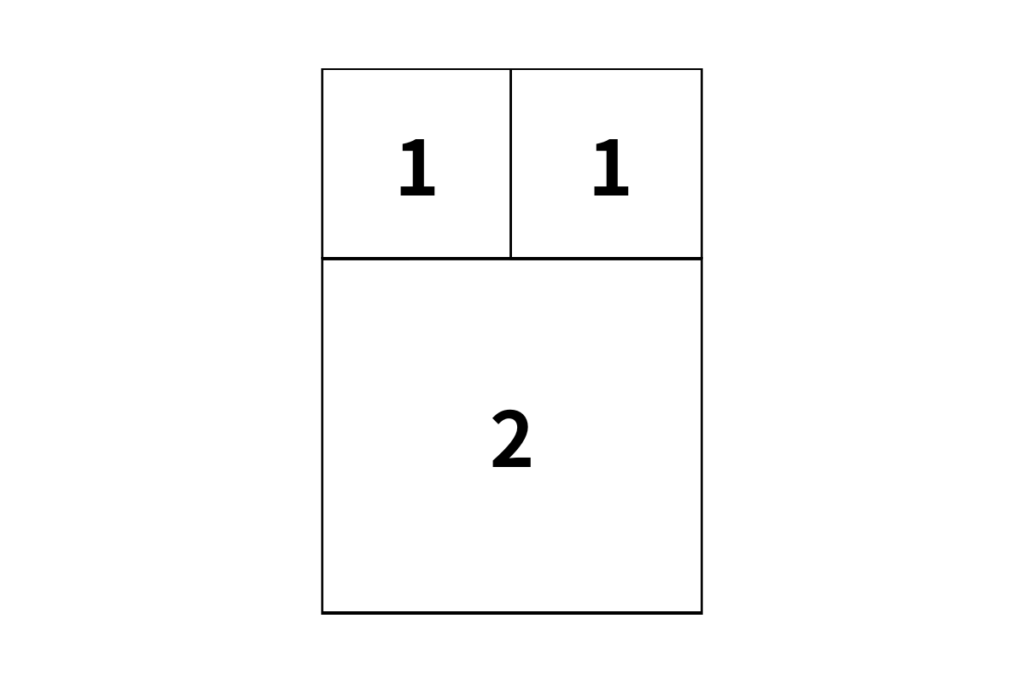

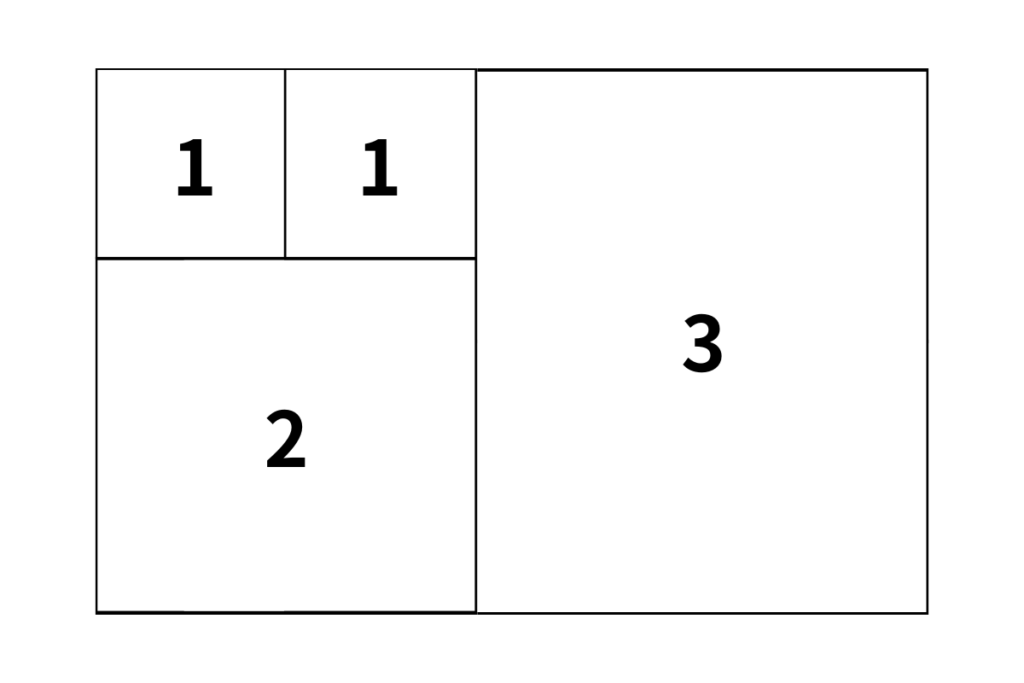

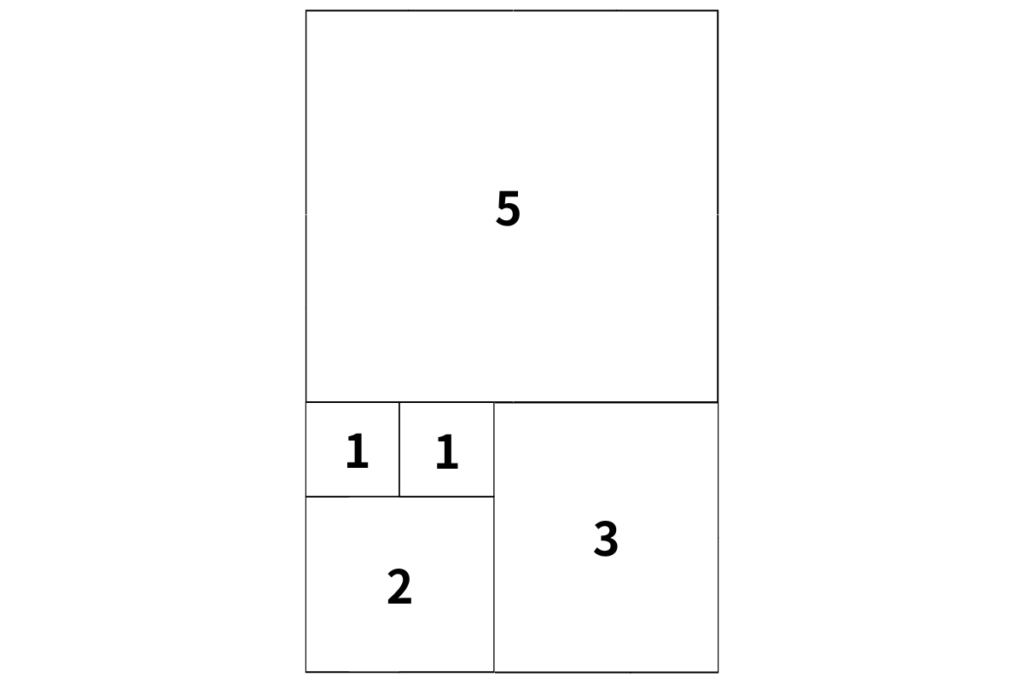

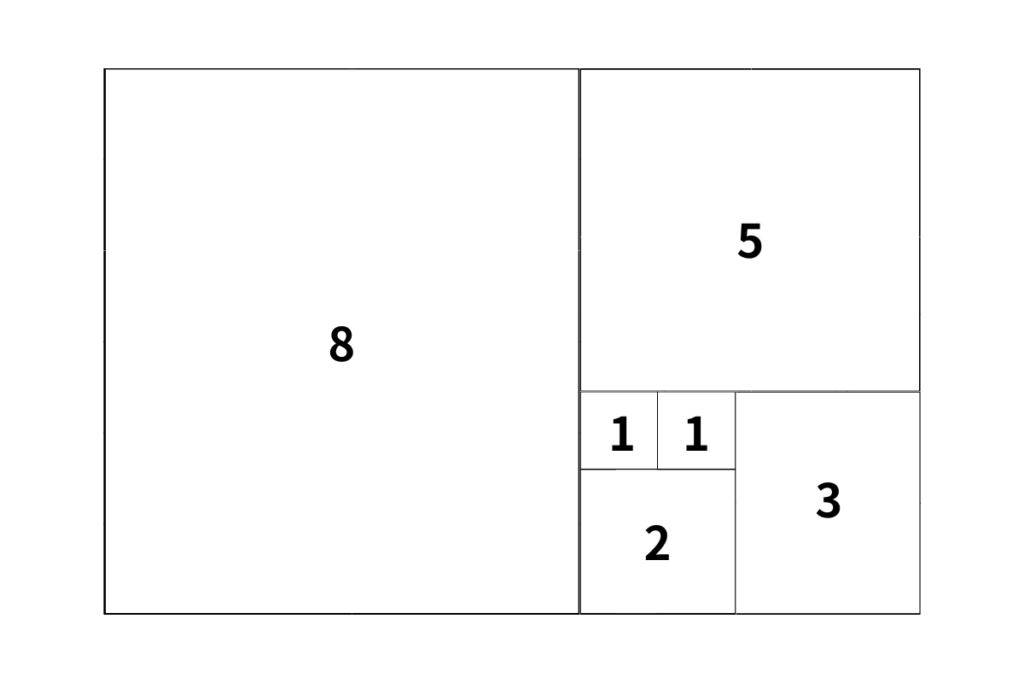

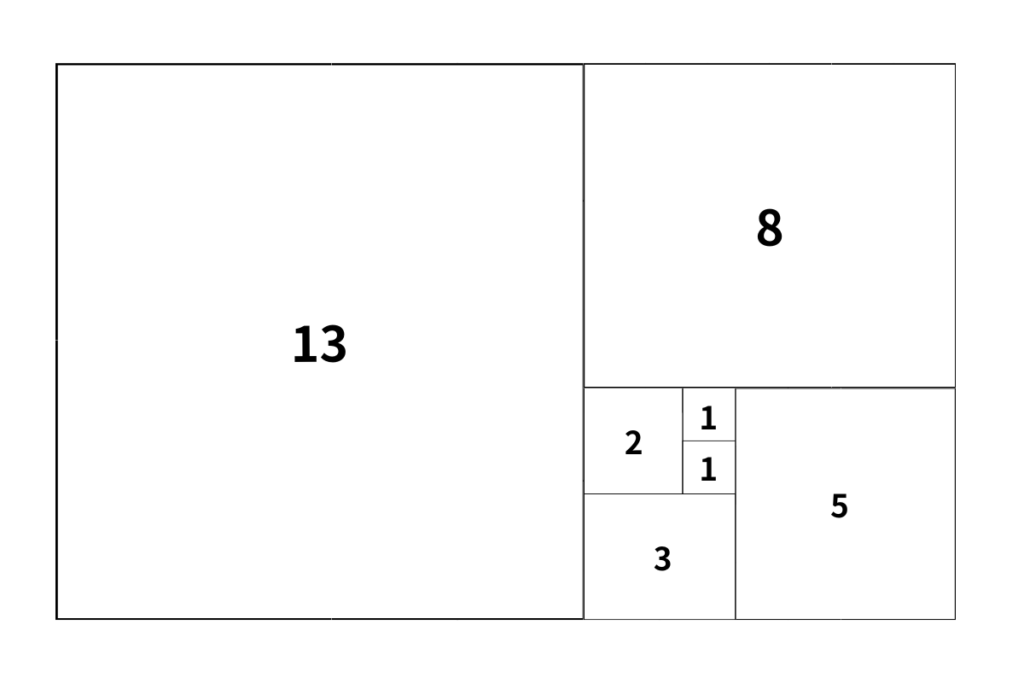

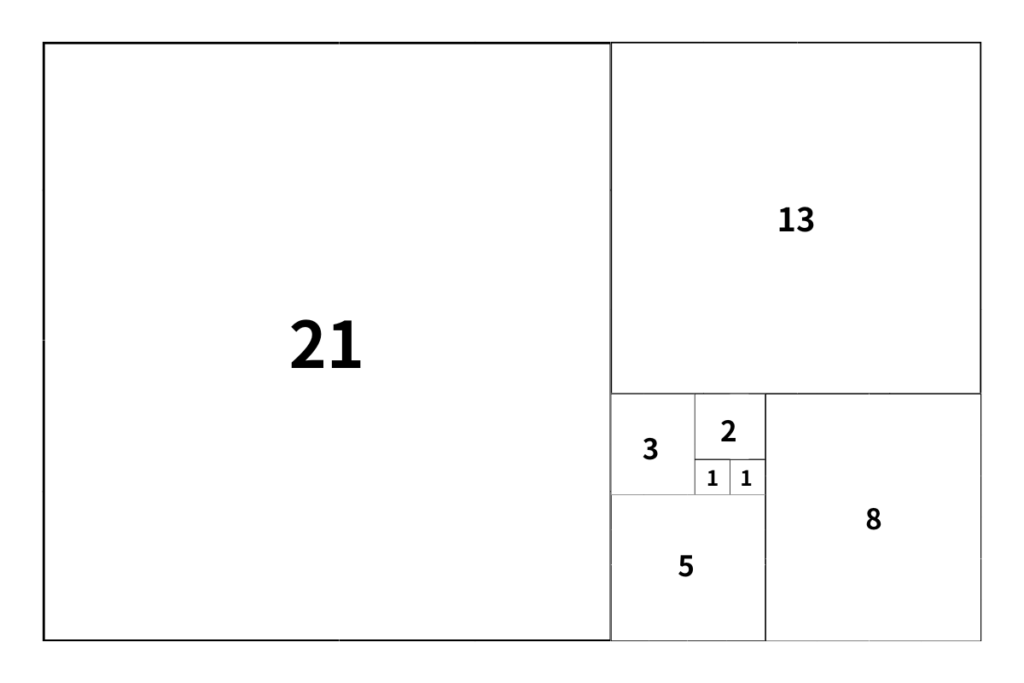

さらにこれらは螺旋を描く形となっているのです。
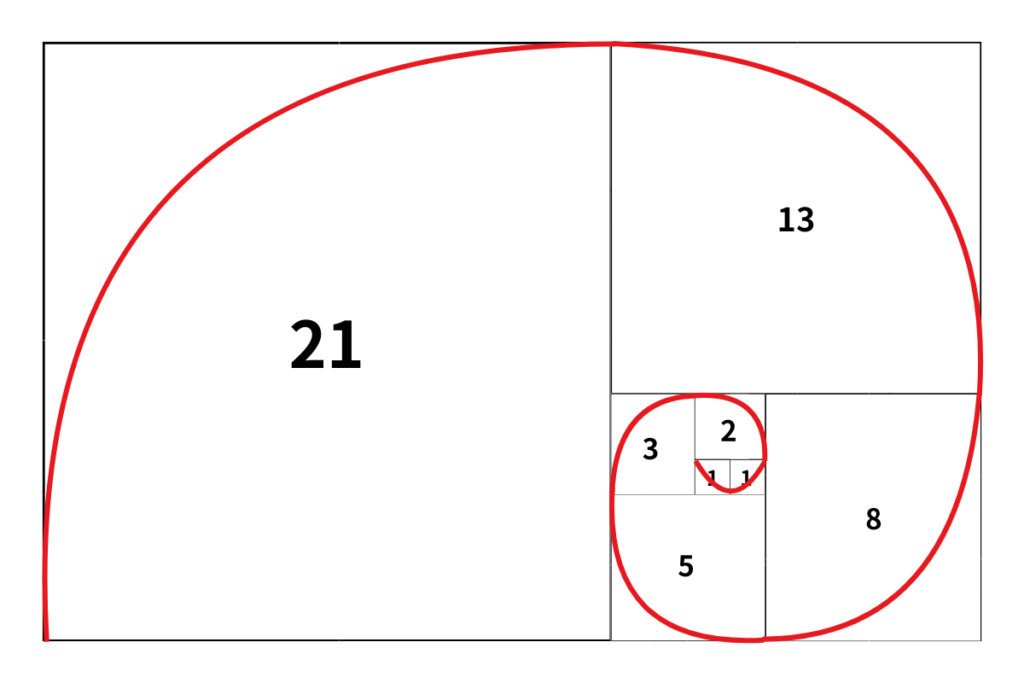

このフィボナッチの螺旋構造は不思議なことに、DNAの螺旋構造や植物の葉の開き方、アンモナイトの貝の模様と同じような形をとっているのです。
植物の並ぶ葉の数や配列、カタツムリの殻、が「1, 1, 2, 3, 5, 8, 13, 21, 34, 55…」と続いているのですね。






動物・植物の中の螺旋構造とフィボナッチ数列の性質がこうも似てくると、もはや自然の中に数学が潜んでいたと考えることもできるのではないでしょうか。
【特徴3】連続する数字は互いに素
フィボナッチ数列の隣り合う数字はお互い1以外で割り切れないという性質があります。
これも非常に面白い性質ですよねぇ〜。
フィボナッチ数列のまとめ
今回はフィボナッチ数列をご紹介しました。
フィボナッチ数列は数字と美の関係性を静かに語る不思議な数の性質です。
フィボナッチ数列を発明した、数学者フィボナッチの生い立ちや人生を紹介した記事もありますので、ぜひ参考にしてみてください。












