「宇宙は数学という言語で書かれている」
天才ガリレオ・ガリレイが残した言葉です。
さらにピタゴラスは「万物は数でできている」とも言っており、数々の偉人が残した言葉を辿ると「数学は神の学問ではないか」と思えます。
僕も高校生の頃、「数学は神の学問だ」という記事を読んで、
 学生マルタ
学生マルタえぇ!?神の学問!?どんな学問だよ!
と心躍らせた記憶があります。
そして、今現在、専門的な数学を学んでいるわけですが、果たして数学は「神の学問」なのか?
またそう言い切る天才が見ている数学は、どんな世界なのか?
そんな疑問のヒントになればと思い、今回は僕の考えを綴っていきます。
【結論】数学は神ではない(※主観)
いきなり面白くない結論で申し訳ありませんw
ですが、正直言えば「数学は神の学問ではない」と考えています。
あ、ただそもそもとして、「神とは何か?」という話がありますが、ここでは神とは「完全なる存在」を前提としたうえで話を進めます。
なぜそのような前提を定めるかというと、
過去の偉人が数学を称賛している理由が、「数学が自然界の法則を表現している」というような、ある種、数学が真理であるというニュアンスを僕が感じているからです。(ここは主観ですm(_ _)m)
そう考えた時、数学が神の学問ではないという結論の根拠は「現在の数学体系では解決できない問題が存在するから」です。
1931年、数学者ゲーデルは「現在の数学体系では真偽を判定することができない問題が存在する」ことを証明しました。
(個人的には、数学でこんなことが証明できること自体が凄いと思ってますw)
また他にも、数直線が繋がっているかどうかも実は証明できているわけでもなかったりします。
つまり学生時代に学んだ関数やグラフも、実は繋がっていないかもしれない?なんていう可能性もあるわけです。



数学では、これらは繋がっているということにしようとされています。
なので、数学は決して万能ではないのです…。
しかし!
それを踏まえても現代の日常や自然法則に数学が使われていることを考えると、数学は人間が真理に近づける可能性を秘めているという意味では、神に近い学問だと考えています。
数学には大きく分けて3つの特徴があります。
1.客観的な学問である
日常生活における議論やコミュニケーションにはない、概念が数学には存在します。
それは厳密なる「定義」です。
この厳密な定義が存在するからこそ、数学は客観性を維持できるのです。
少しおおざっぱな例ですが、日常会話で、「いやぁ〜、昨日は仕事頑張ったな〜!」と発言したとします。
しかし、人によっては「頑張った」の基準は違いますよね。
取引先への挨拶周りを最低3件はこなし、契約も1日1件達成できてはじめて「頑張った」と思える人もいれば、
1日仕事を無事終えることができたことに対して、「頑張った」と評価する人もいるわけです。
つまり、「頑張った」という表現の受け取り方は人それぞれ違っていて主観的だということですね。
(※「頑張った〜!」「いやそれは甘えだね。まだ頑張りが足りないね」みたいな議論が起こる原因は、主観によることが大きかったりします。)
一方、数学の場合は「頑張った」を厳密に定義します。
簡単に言えば、「〜〜の状態を頑張った」というルールを決めるのです。
そのようなルールを決めることで、100人中100人が同じ認識で「今日は頑張った!」「頑張れなかった」と言えるわけです。
このように数学では定義を決め、100人中100人が「そうだね」「違うね」と判断できる厳密な定義の上、議論や証明がされています。
この徹底した客観性が、数学の特徴の1つです。
2.普遍性ある公式・定理
中学・高校、あるいは大学で学んだ数学の公式はたくさんあると思います。
当時の僕は、「ふーん」ぐらいな感想でしたが、今振り返ると公式の1つ1つが凄いなぁと感じております。
公式や定理が生まれる背景はいろいろありますが、決定的なのは「普遍的」であるということです。
学生の頃に学んだ「三平方の定理」を覚えてますか?
別名、「ピタゴラスの定理」と言われますが、こんな公式です。
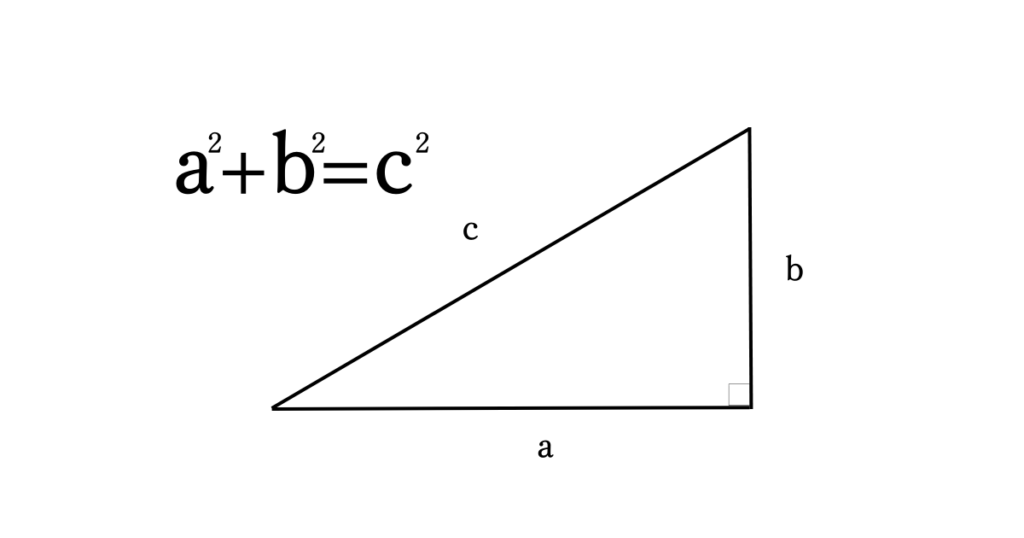
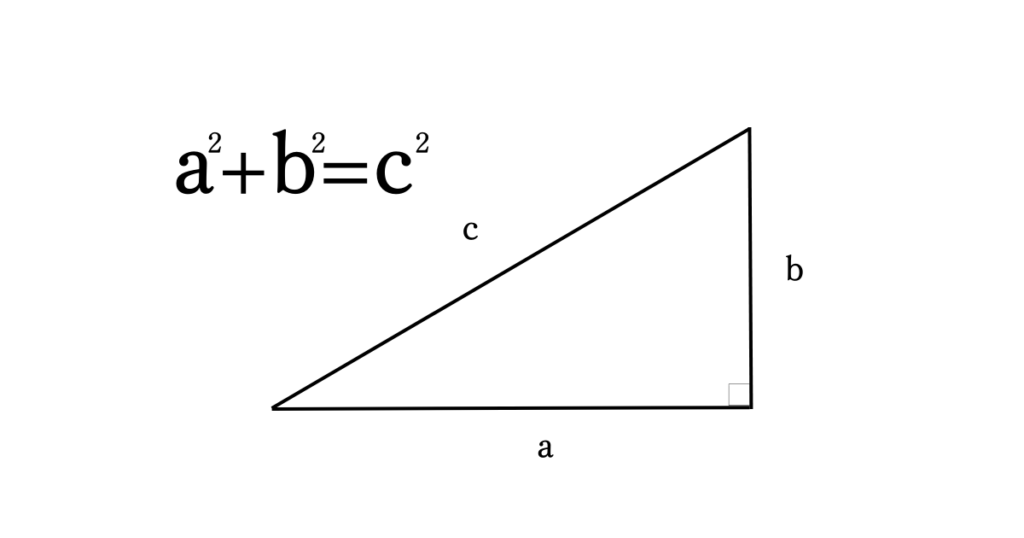
この方程式が成り立つ三角形は直角になるのです。絶対に!
例えどんな大きな直角三角形でも、どんな小さな直角三角形でもこの法則が成り立つのです。絶対に!!
絶対ですよ、絶対!!
凄くないですか?
絶対なんて絶対ない、という言葉を聞いたことがあるのですが、「数学には絶対があるぞ!」と教えてやりたいですね笑
ちなみに、ピタゴラスの定理は紀元前1800年頃には発見された定理だそうです。(諸説あり)
なので、数千年の時が経った現代でも、この定理は変わっていないことになります。
天動説から地動説になったり、宗教改革が起こったり、コロナで生活が激変したりと、世界がどれだけ変わっても、定理は変わらなかったのです。
もちろん、数学における他の全ての定理・公式は普遍的です。
何年経っても変わらない。
これが数学が持つ普遍性です。
数学の定理が唯一変わるとすれば、数学が前提としている公理が変わる時だけです。
これさえ変わらなければ、数学の定理は普遍という一応の補足です。
とはいえ、公理系も言葉や表現は変われど根本は変わっていないことを考えれば、これからも変わる可能性は低いと考えます。
3.無限(≒神)の概念を扱える
僕が好きなテーマの1つでもある「無限」。
大昔から、「無限」という概念は「神」や「真理」と考えられており、多くの数学者が畏敬の念を抱いていました。
大災害から自然への畏敬の念を抱くように、数学者は無限から論理への畏敬の念を抱いていたと言えるかもしれません。
そんな神や真理と言えるような無限の概念を数学では論理的に扱うことができるのです。
ただ無限には直感的には理解不能ないろんな不思議性質が存在します。
無限のテーマで特に驚くのは「無限には大小」が存在するということ。
これは無限大(限りなく大きい)や無限小(限りなく小さい)だけでなく、無限大の中にも大小が存在するという意味です。



な、何を言っているんだ!?
と感じたかもしれません。僕も同感です。
無限大と聞くと、無限大でしかないでしょうと。
しかし、そうではないのです。
天国という概念の中にも、さらに低層と高層が存在するように、無限に大きい数字の中にも小さい・大きいが存在するわけです。
このあたりは、説明すると長くなるので割愛しますが、無限の中にも大小が存在するというのは、直感的には理解できません。
しかし、このような直感的に理解できないことも、数学の論理で考えることができるのです。
これは目で見えない神をも、数学によって完全に解明できる、かもしれないという可能性を秘めていると考えられます。
まとめ〜数学は神の学問ではないが、想像を超越したことを論理的に考えることができる点では真理に近いと言える
というわけで、数学は決して神でも万能でもありません。
それは、不完全であることが証明されたからです。
しかし、だからと言って数学の全てが嘘であるわけでもありません。
あまり知られていませんが、実は数学では「数学を表現する新しい数学言語」も発明されているのです。
(圏論などは戦後に登場した比較的新しい数学分野です。)
なので、現在の数学は不完全かもしれませんが、人類の思考が発展していき、新しい数学体型が構築されれば、いつかは「神の学問」になれるのかもしれません。
その日が訪れるのをのんびり待つのが良さそうですね。