先日、「センスオブワンダー」という書籍を読んだのですが、非常に純粋な本だなぁと感銘を受けました。
センスオブワンダーとは、レイチェルカーソンが書いた書籍。
子供の無邪気さ、純粋さ、何事にも飽くなき好奇心を持つ「センスオブワンダー(神秘の感覚)」を持つことの重要性。
大人になるにつれ失われゆく感性を、いつまでも大切にし続けることが大事だと述べられている名著です。
読んでて、ふと数学的なアイデアが生まれたので、
自然たっぷりの書籍に論理を持ち込むのは心引けるが、センスオブワンダーを数学的に考えてみました。
その前に、僕の身近な自然の神秘を紹介します。
僕の散歩ルートの1つに「大濠公園」があるのですが、
おそらく「福岡市」と検索するとトップに出てくるような、地元では有名な場所です。

この大濠公園は、自然豊かな光景が広がっています。

四季によって姿を変える自然が存在するのである。
春にチラホラ現れるサギ

夏に現れる亀たち

秋から冬にかけて増殖するカモ(逆に亀たちはどこかでいく)


同じ場所なのに、自然のサイクルがあって非常に不思議だな〜と感じるわけです。
春にサギが現れ始め→夏には亀が増え→秋〜冬にはカモが増える→春にサギが現れ始め→夏には亀が増え→秋〜冬にはカモが増…
と、地球が破滅するまで、このサイクルを無限に続けるのでしょう。
これが僕の身近にある自然の神秘なわけですが、
この経験とセンスオブワンダーを読んで、1つの考えが頭に浮かびました。
さては!!
これは「数直線の話か!?」と。
ここで数学の話をしましょう。
数は数直線上の点として表現できます。
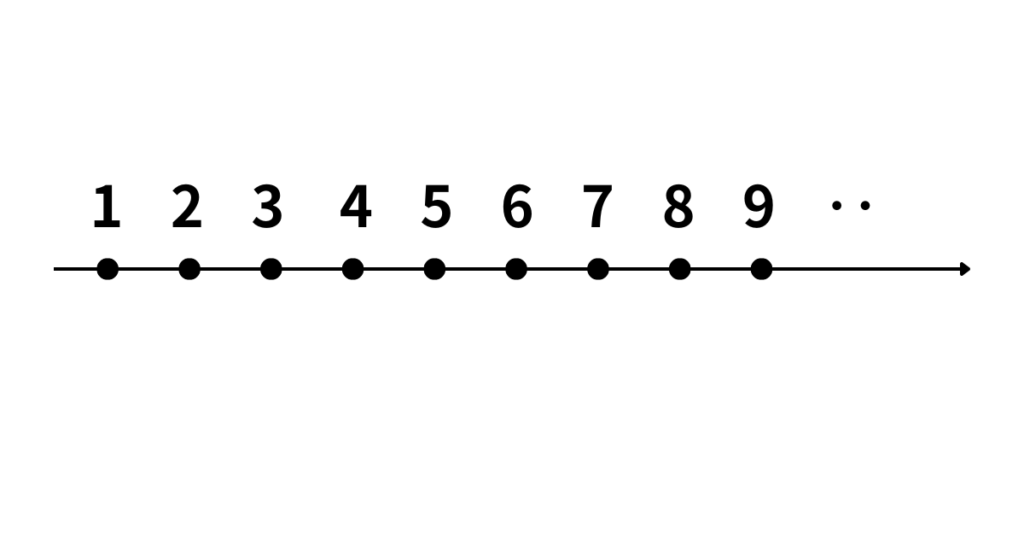
1,2,3,4,5…と無限に広がる数の点が存在する。おそらく数字と聞いてパッと思いつく数字の列であろう。
「じゃあ数字はこれだけか?」と言われれば、そうではなく。
1,2,3,4,5…と無限に広がる数の点が存在しています。
おそらく数字と聞いてパッと思いつく数字の列だと思います。
「じゃあ数字はこれだけか?」と言われれば、そうではなく
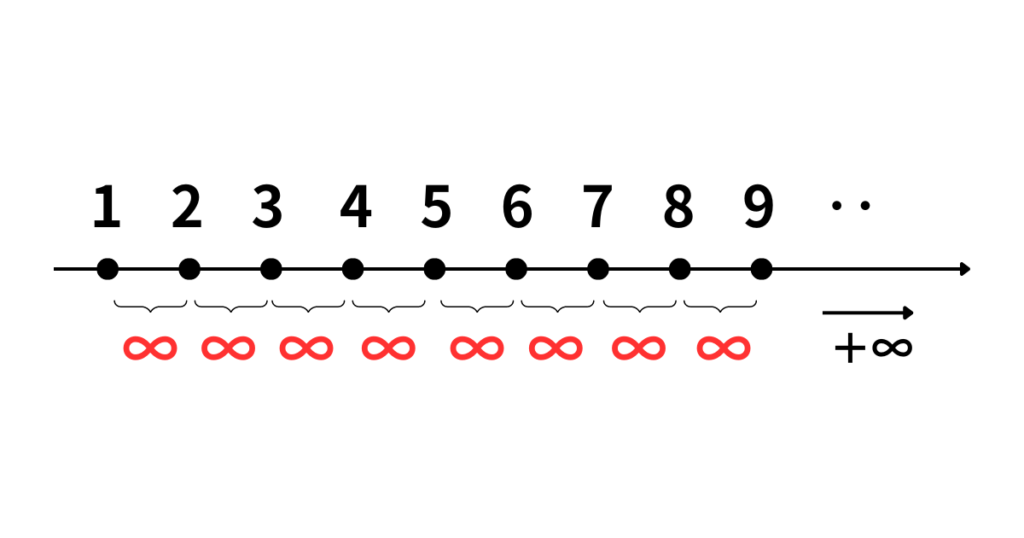
実は1と2の間、2と3の間など、、、
2つの数の間には、目には見えないが確かに数字が存在しているのです。
例えば、1.1や3/2(=1.5)、3.9999999999などなど…
その数はなんと無限個。
ここで僕が大濠公園で体験した自然現象を点として表現することにしてみましょう。

数直線と同じ理論で考えたなら、
これら自然現象の間にも、目には見えない自然現象が無限個に存在するのではないか。

そこで僕はセンスオブワンダーは、
目に見える現象だけでなく、
「現象と現象の間の目には見えない現象を感じ取る大事さ」も語っているのではないか?と考えたわけです。
センスオブワンダーの文章が美しく感じるのは、ありふれ過ぎて見過ごされそうな現象にスポットを当てているからだと感じています。
例えば、センスオブワンダーの1文を抜粋。
メイン州の森は、雨が降るととりわけ生き生きとして鮮やかに美しくなります。
針葉樹の葉は銀色のさやをまとい、シダ類はまるで熱帯ジャングルのように青々と茂り、そのとがった一枚一枚の羽崎からは水晶のようなしずくをしたたらせます。
ザックリ言えば、雨に濡れた葉を表現しているわけです。
普通なら「葉っぱが濡れてるわ〜」とスルーしそうな光景だが、その光景にありったけのスポットライトを当てているわけです。
※もっと言えば、「さやをまとい」「しずくをしたたらせる」という表現は能動的な述語なので、主語である葉っぱに命が宿っている印象すら感じられます。
話を数字に戻します。
パッと思いつく、「1」や「2」という日常的に使う数字だけじゃなく、数字の間には普段は意識しない数字も存在します。
普段の生活ではどうでしょうか。
どうしてもパッと目に入る表の現象や出来事、情報に目を取られがちだが、その裏にも目立たない数々の現象は存在するわけです。
例えば、
「やった!明日休日だ!」と感じることができるのは、働くべき平日が存在するからである。(毎日が休日なら、イベントでもない限り、休日を楽しみにする喜びは失われる。)
刺激を楽しめるのは、良くも悪くも退屈が存在するからである。
(毎日が刺激的なら、きっと刺激を楽しめなくなるだろう、より上位の刺激を堪能すれば、以前までの刺激は刺激ではなくなる。)
朝日の光をありがたく思えるのは、夜が存在するからである。
自由を望むことができるのは、不自由が存在するからである。
(毎日が本当に自由なら、自由という概念すら消える。)
そう考えると、目立つモノをありがたいと思えるためには、目立たないモノが必要。
ということは、目立たないモノにもありがたいと思えてくる気がする。
日々の退屈さこそが、刺激をより一層刺激たらしめる要素だし、
裏を変えせば、退屈さがあるからこそ刺激が目立つ。
そう言えるのではないでしょうか。
世の全てに溢れるキラキラするもの。
目に見える現象が存在できるのは目には見えない、光のない現象のおかげ。
つまり相対的な概念が2つあるからこそ、存在できるわけです。
そう考えると、
目には見えない現象にも光(=意識)を向けようと思えてくるのではないでしょうか。
しかし、今まで目には見えなかった対象に目を向けると、今度は相対的に目には見えない対象が新しく生まれる。
その新しく生まれた対象に目を向けると、また相対的に目には見えない別の対象が生まれる。
さらに新しく生まれた対象にまた目を向ける…
と繰り返せば、不思議なことに無限に分割できるのではないでしょうか。
そう感じた時、僕の大濠公園での体験を思い出しました。

サギが現れる、亀の群れが現れる、カモが急に増える。
今まではこれらは現象は点として捉えていましたが、きっと見えない自然の因果が存在するのかもしれません。
春にサギが現れるから、夏には亀が現れるし、夏に亀が現れるから、秋〜冬にはカモが増えるのかもしれません。
これらの現象が全て因果によって連続的に繋がっているのなら、現象と現象の間には無限の自然現象が存在し、
それによってもたらされる連続性こそが、アナログであり、自然なのではないか。
と思ったのです。
この大濠公園の自然体験はあくまで、1つの例に過ぎないません。
日々過ごす家、空間、場所、関わる人々。
現象と現象の「間」をいかに感じ取れるかが大事なのかな〜、と。
目立つモノに目を奪われがちだからこそ、その間に無数に存在する目立たないモノを多く感じ取って生きていきたい。
そんな本だったなと感じました。