どうもマルタです。
ある日、洗濯物を干している時に人生初のギックリ腰になりまして。。。
痛みで歩けず、数日間ずっと布団にこもりっぱなしで過ごしておりました。
あぁ、、、歩けるって幸せなんだなって改めて感じましたねぇ(今はもう完治しました)。
布団の中でぼけーっと思っている時に、ふと思ったんですね、
「福岡タワーの体積ってどれぐらいだろ?」って。
※ちなみに、福岡タワーとはこのような電波塔で福岡市のシンボルの1つです↓

なぜ福岡タワーの体積を考えたのか?それはわかりませんが、きっと僕の魂が求めているのでしょう笑
調べてみたのですが、福岡タワーの体積の情報なんてまぁ出てこねぇ・・・。(まぁ当たり前か。)
せいぜい延床面積ぐらいですわ。
「仕方ねぇ!自分で計算するしかねぇ!」と思いたち、福岡タワーの体積を導き出す経緯をつづろうと思い筆をとった次第です。
古代ギリシャの哲学者タレスがピラミッドの美しさに魅了され、高さを測ったように、
僕もその精神を見習って、
シンメトリーで美しい福岡タワーの体積を求めてみようかなと思います。(高さは調べれば出てくるので面白くない)
とはいえ、今回は厳密ではなく、およそで調べています。
途中、あいまいな仮説も含まれることをご了承くださいm(_ _)m
体積を求める方向性
まず福岡タワーの形はこんな感じです。
若干いびつですが、頑張ればなんとかなりそうかなって感じですかね。
真横アングル


後ろアングル

今回求めたいのは以下の部分。

もっと簡略化するとこんな感じで表せます。(真横から見た場合)
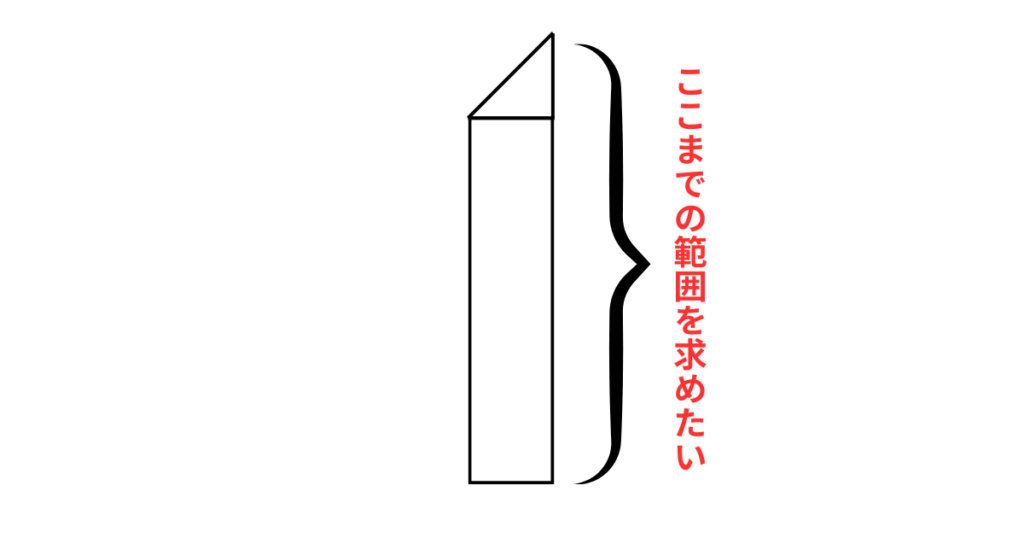
福岡タワーは、上の部分が少しいびつな形をしています。
ですので、体積を求めるには、まずは福岡タワーを分解します。
すると「三角柱」と「四角錐」に分解できます。
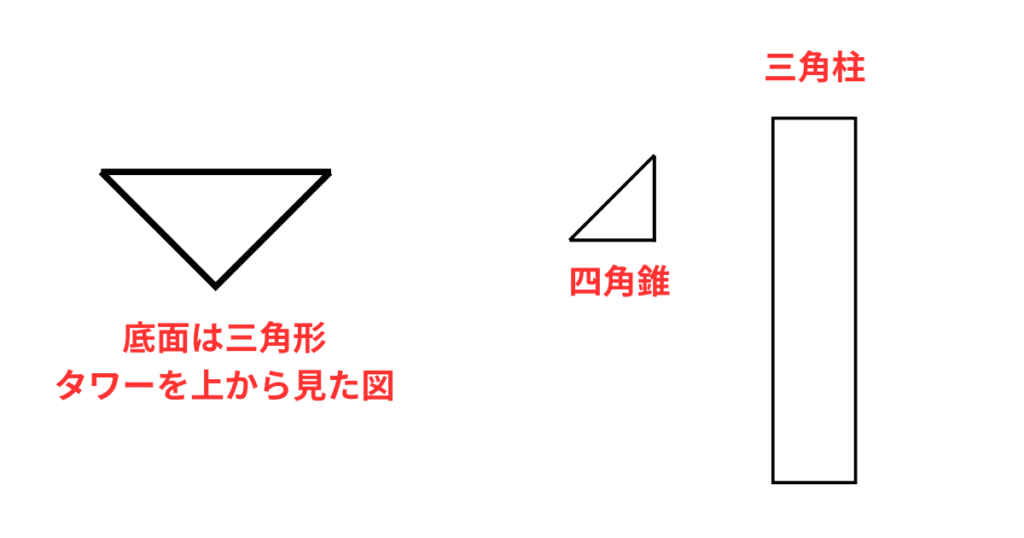
ちなみに、真横から見たら三角形、四角形に見えますが、上からみると三角形の形です。
つまり、求めるためには、
三角柱の体積を求めるー①
四角錐の体積を求めるー②
そして①と②を足せば、欲しい体積が出てきそうですね。
これで体積を求める方向性が決まりました。
未知数と既知数を分類
方針が立ったら次は、未知数と既知数を分類します。
ザックリ言えば、わかってる数字とわからない数字を把握することですね。
そして、わからない数字を求めていけば答えに辿り着くことがわかります。
わかっている数字を調べるには、インターネットの力を借りましょう。
ってことで調べてみると以下の情報が手に入りました。
116 – 123mの高さに展望階の3・4・5階(第31・32・33層)がある。
建設地:福岡市早良区百道浜2丁目902番5
敷地面積:12,000㎡
建築面積:3,093㎡
延床面積:6,080㎡
高さ:最高の高さ GL+234.00m :展望台の高さGL+123.61m
>116 – 123mの高さに展望階の3・4・5階(第31・32・33層)がある。
これはザックリ言えば、福岡タワーの最上階(展望フロア)まで33層だということですね。
ちなみに、情報源は福岡タワーの公式サイトとWikipediaです。
Wikiってどうなの?と思ったのですが、上記の数値は
福岡市経済農林水産局博覧会推進対策室/編集『福岡市活動記録:アジア太平洋博覧会-福岡’89』福岡市経済農林水産局博覧会推進対策室、1990年、85頁
から引用しているということで、OKでしょう。
しかし、残念ながら、、、この敷地面積、建築面積、延床面積はあてになりません。
なぜなら、福岡タワーにはお店が併設されており、この併設された面積も含まれている可能性があるからです。
(この辺りの詳細情報は確認できなかった。)
僕が知りたいのはあくまでタワーのみ!となれば、既知の数として使えるのは、
①既知の数を考えると、展望台までの高さは123m
②展望フロアまで33層でできている

くぅッ!一気に使える情報が減った!
一方未知数と言えば、タワーの横の長さ。

いやいや!これ一番欲しい情報なんですけど!それが分からないとは、、、
サクッと体積求まるかと思ったが、どうやら一筋縄じゃいかなさそうだ。。。
難しいからこそ、探究しがいがあるってもんだ!
手がかりを探す
「あぁ、福岡タワーの横の長さが知りてぇ…」と空を見上げた時に思いつきました。
あれ?福岡タワーの外壁ってどうなってる?
手がかりとなったのは、福岡タワーの外壁に貼られているガラスでした。

よく見たら、規則正しく正方形のガラスが貼られてるじゃん!
ということは、このガラスの横の長さがわかれば、タワー全体の横の長さもわかる!
このガラスの正体を突き止めるべく調べた結果、このガラスは「森硝子店」という企業が提供しているとのこと。
当時は、過去最大規模のプロジェクトだったようです。

スタッフのコメントからは人間味溢れてくる。

引用サイト:http://mori-glass.co.jp/business/results/01.php
森硝子店さん、、、アンタの思い無駄にしねぇ!!
そう決意して、ガラスの横の長さを考えることにした。
多少の誤差は多めに見るとして、、、
まずは1フロアの高さを測ろうと思ったが、Wikiによると
3階(第31層、116m):展望室
4階(第32層、120m):スカイラウンジ ルフージュ(食事・喫茶)
5階(第33層、123m):展望室
つまり31層から32層までは4m。
32層から33層までは3m。
「バラバラやないか!」ということで、1層の平均高さを求めることにした。

※ちなみに、1層は黒線と黒線に囲まれたこの範囲
1層に対して、縦のガラスの枚数は4枚。(画像を見て数えた)
全体の高さ123mに対して、33層あるので、1層あたりの高さは平均3.7m。
ということは、1枚のガラスの高さはだいたい3.7÷4で0.925(m)
悩んだ挙句、今後めんどくさくなりそうだから高さ約1mで考えます。
これでガラス1枚の高さが約1mであることがわかった!
ガラスは正方形だから、ガラスの横の長さも1mぐらいだろ!
ん?本当に正方形か?
画像をみる限り、ガラスは正方形…だよな?
なんだか嫌な予感がした。


ガラスって正方形か?
正方形だよな?
正方形であってくれぇ!
僕は祈った。
そして、スマホで撮った過去の写真を調べて見た結果、、、

どう見てもガラスは長方形でした…orz
つまり高さとは別で、横も求めないかん。
でもどうすれば?腰痛いから現地へは行けない。。。
あぁ、これでついに終わったか…。
せっかく横の長さを測るキッカケを掴んだのに、これで終わるのか…。
そんな時、1つの仮説が。
福岡タワーは非常に綺麗なシンメトリーである。
つまりは、それほどまでに美しさにこだわっている証拠。
であれば、そんな審美眼を持った人たちが作った建造物である。と信じたい。
ならば、きっとアレを活用しているはずだ!!
そう「黄金比」!!
黄金比とは、1:1,618の対比で表される、美しいとされる比率のことです。
つまり、ガラス1枚の高さがおよそ1mならば、横の長さは1.6mであると信じたい。
というか、そういうことにして欲しいw(じゃないと計算が進まない汗)
ということで、ここからはガラスに黄金比が使われているという仮定で話を進めます笑
ガラス1辺の横の長さが1.6m。
福岡タワーの横に張り巡らされたガラスの枚数は17枚。(これは画像をアップして数えた)

ということは、1.6と17をかけたら横の長さが導かれる!
1.6×17=27.2(m)
これがずっと知りたかった福岡タワーの横の長さである。
さて、ようやく計算ができるぞ!
ということで、あとはゴリゴリ計算するのみです。
いざ、計算!
ここからは計算パートに突入です。
福岡タワーを四角錐と三角柱の部分に分けます。

まずは三角柱の体積を求めたいと思います。
三角柱の体積
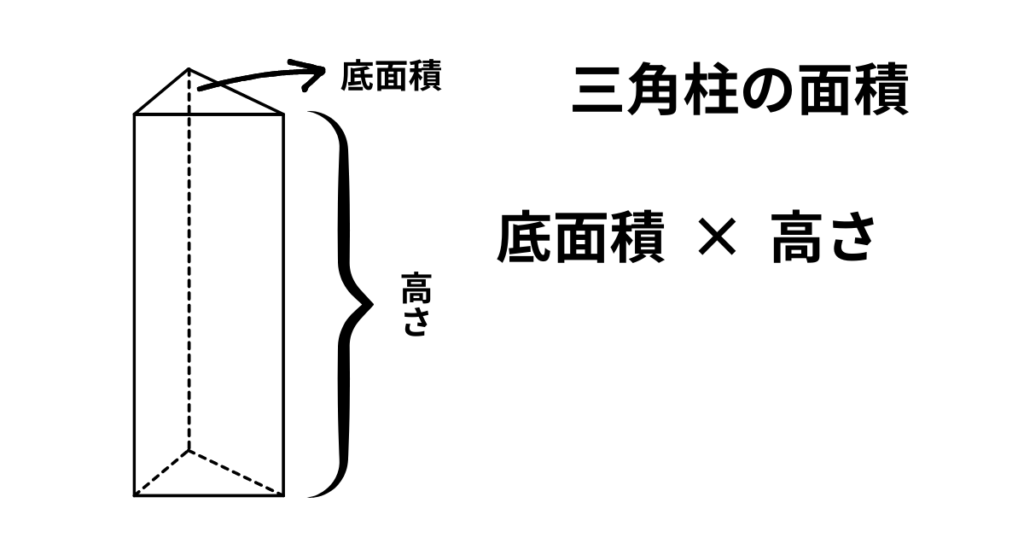
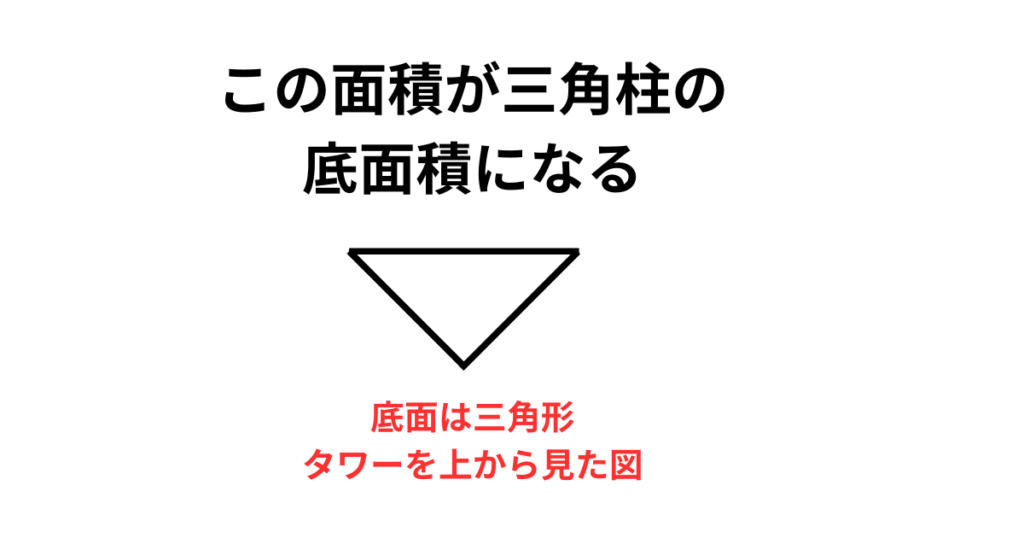
タワーの外側に貼られているミラーの数は3辺とも同じ数で配置されています。
ということは、底面の三角形は3辺が同じの正三角形と考えることができます。

正三角形の面積は、(底辺)×(高さ)÷2で求まります。
まずは三角形の中の高さを求めましょう。
1辺をaとおきます。
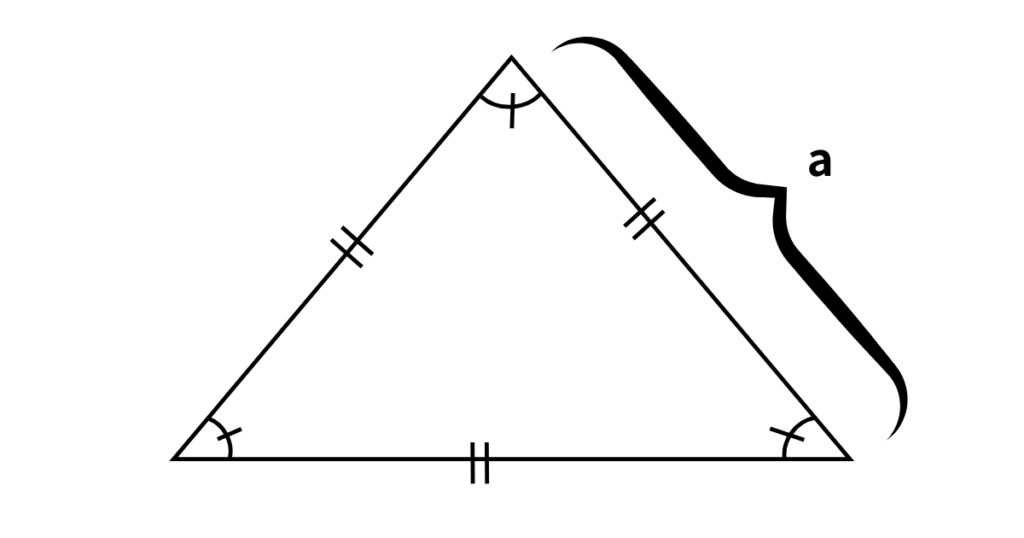
正三角形の中心に線を引きます。(これが三角形の中の高さとなる)
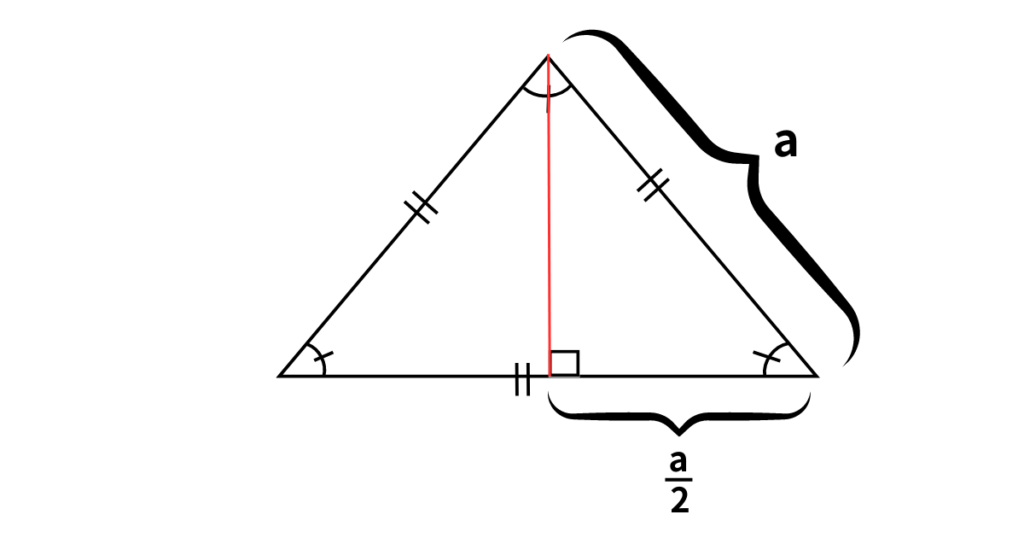
ここであの必殺技を使いましょう。
その名も「三平方の定理」
ピタゴラス!俺に力をーーー!
三角形の中の高さをxとおきます。

よって三角形の中の高さxが求まりました。
ゆえに底面積(=三角形の面積)は、


※少し前に求めたタワーの横の長さ(=27.2)は、三角形の1辺の長さでもあります。
これで三角柱の体積が求まりそうです。

展望フロアまでの高さは123mなので、

次に、タワーの四角錐の体積を求めていきます。
四角錐の体積
これまで使ってきた123(m)はあくまで地上から展望フロアまでの高さです。
では展望フロアからトップまでの高さはどのように求めるか。

展望フロアより上の層から一番上までのガラスの枚数は20枚。
そして、ガラスの高さはおよそ1mなので高さ20mと導き出せます。





とりあえず一応求めてみましたが、合っているかどうかは分かりません笑
検証もめんどくさいのでやってないです汗
総括
ということで、今回は福岡タワーの体積を測ってみました。
普段あまり気にしないことを考えてみるのは、めちゃくちゃ楽しいですね〜。
おかげで福岡タワーの体積だけでなく、歴史や関わっている人々のエピソードを知ることができました。
もし途中の間違いや、他の解法あれば教えてくださいm(_ _)m
人間はもしかしたら、たとえ意味のないことだとしても、自分で問いを立てて解決することに幸福を覚えるのかもしれない。
そう感じた贅沢なひと時でした。
途中で登場した人物タレス、ピタゴラスに関する記事はこちらで詳しく解説しております。
興味があればぜひご参考ください。
最後までお読みいただきありがとうございましたー!