どうも、マルタです。
以前、こちらの記事で「容疑者Xの献身」について解説しました。
該当記事はこちら
【数学徒然草】ネタバレなし!容疑者Xの献身で印象に残ったこと
この作品の中で登場した「幾何に見せて実は関数の問題である」という言葉が登場します。
作中では石神は数学の教師で、テストでは「幾何に見せて実は関数の問題」というひっかけ問題を出すのだそうです。
ただこれは表面的な意味で「幾何の問題のように見えて、実は関数の問題」というのは問題だけではありません。
物語においては主に比喩表現として使われており、つまりは「思い込みの盲点」を意味しています。
石神が施したアリバイトリックは、一見するとAの道順を辿れば犯人にたどり着くような設計になっています。
事実、見つかった物的証拠もAルートへの確信を強くするような物ばかりでした。
しかし、実は正解はBであり、Aのルートを深く追求すればするほどにドツボにはまり、やがて抜け出せなくという物なのです。
作中では、まんまの引っかかった警察が証拠となる最後の決定打が掴めず悩んでいる様子が伺えます。
という「幾何に見せて実は関数の問題」を実際に作ってみようと思った次第です。
とりあえず作ってみた
幾何に見せて、実は関数の問題…。
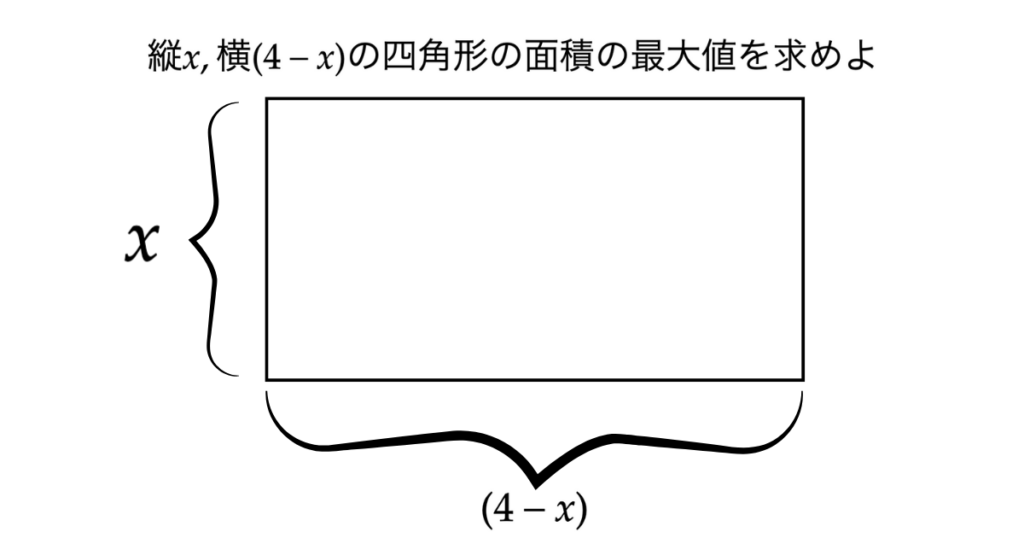
そこでパッと思いついた問題がこちら。
解答はこんな感じ。

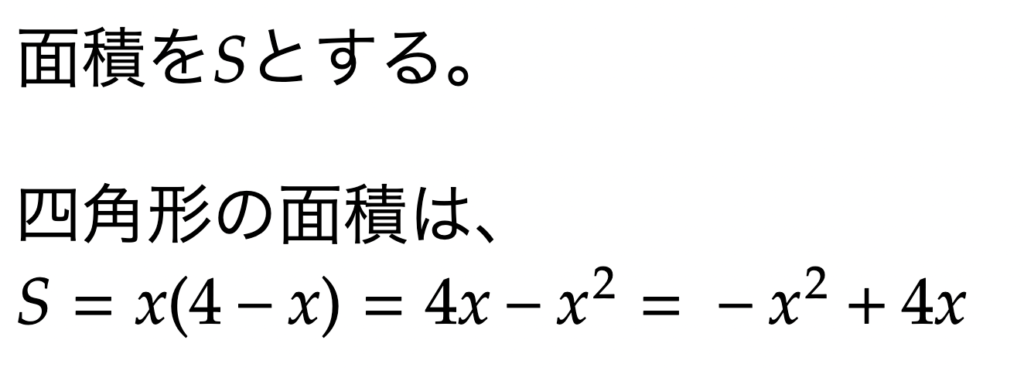

グラフに落とし込む。

よって、xの値が2のとき、面積の最大値4となり二次関数で答えが導き出せます。
これは幾何学から始まり、関数で解がもとまる問題の事例かな〜と。
でも、なんだか単純すぎやしないか?
石神が言っていることってこうじゃないよな。
ここで石神のセリフを思い出す。
「難しくはありません。単純な引っかけ問題ばかりですよ。例えば、幾何の問題のように見えて、実は関数の問題だとか。少し見方を変えれば解けるはずなんです。」
つまりは石神の意図する「幾何の問題のように見えて、実は関数の問題」はひっかけ問題であることがポイント。
多くの人は「これは幾何学的に解くのだろう!」と思っていたが、「なにぃ!?関数だと!?」と驚嘆するような問題である。
そんなひっかけ問題どうやったら作れるんだ?
数日考え込んだ。
そして、こんな問題が思いついた。
幾何に見せて実は関数の問題作ってみた
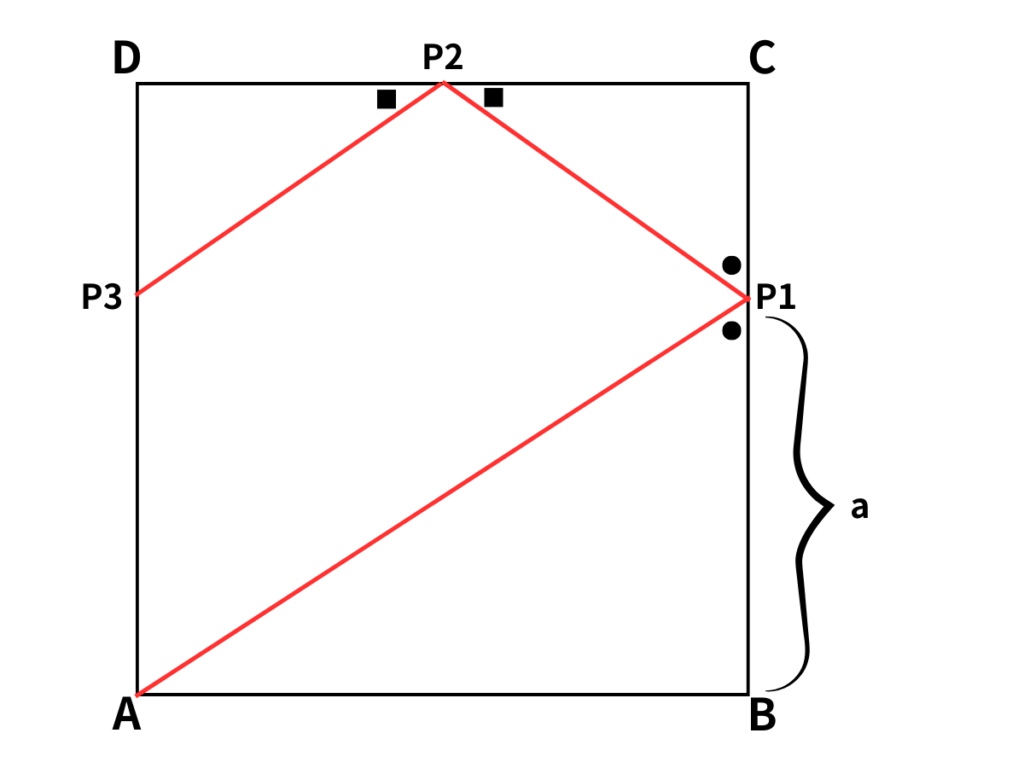
1辺が1の正方形があり、角をそれぞれABCDと設定する。
それぞれの辺AB、BC、CD、DAは鏡でできている。ここでAから光を辺BCに向けて発射する。辺BCは鏡なので、反射した光は辺CDへ向かって反射する。
さらに辺CDにて光が反射し、DAへ向かう
反射したポイントをそれぞれP1、P2、P3とする。この時、光の進んだ経路、AP1+P1P2+P2P3の長さを求めよ。
解答編
では解答を綴って参ります。
まずこの反射をどう考えるか。

この反射をさらに反射させるとアプローチがシンプルになります。
以下にように考えます。
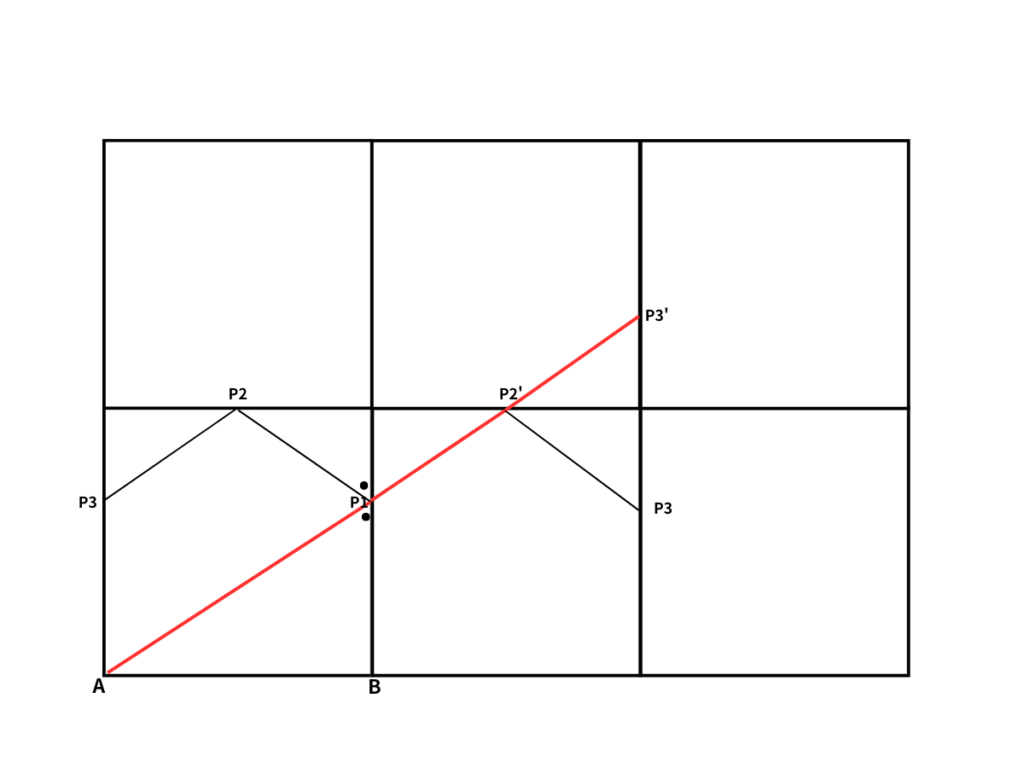
P1とP2を水平方向に対称させると、P1P2’となります。
そして、P2’P3を鉛直方向に対称をとると、P2’P3’となります。
そうすると求める経路は、AP3’の一直線となります。
以下のようにCを設定すると、三角形ACP3’は直角三角形となるので、「三平方の定理」が使えます。
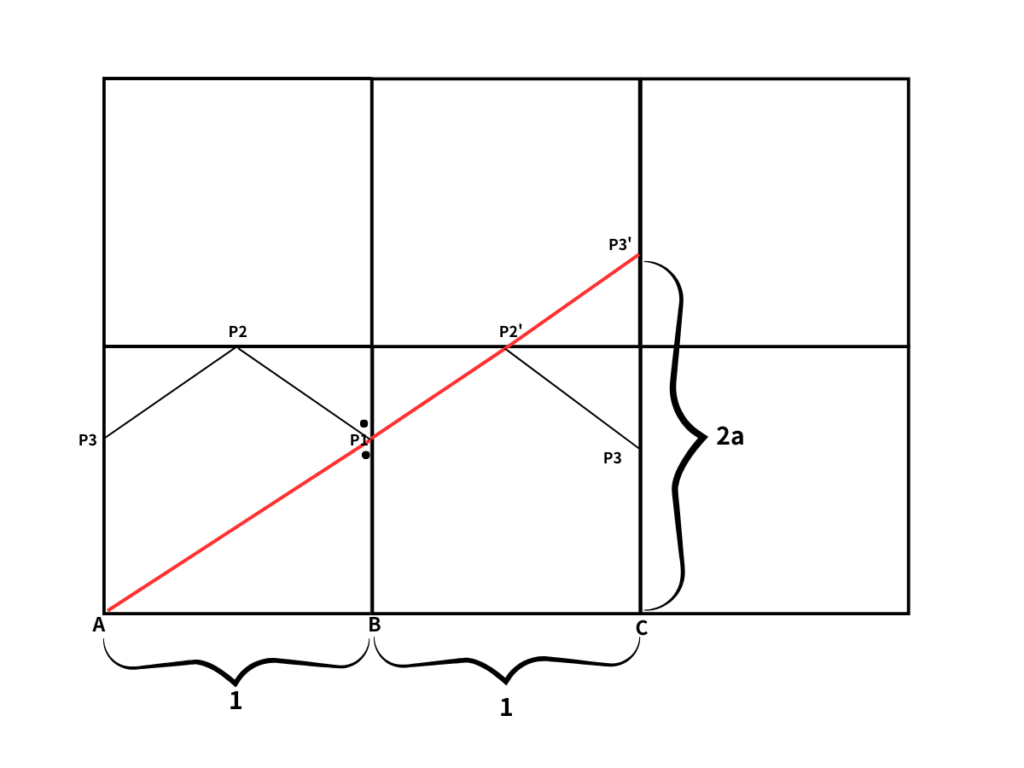
AP3’の長さは(ACの2乗)+(CP3’の2乗)をして、最後ルート(√)を被せれば求められそうですね。
ここで、1つの正方形の縦横はともに1なので、ACの長さは2。
CP3’の長さは2aとなります。
なぜ2aになるのか?それはこの図形を関数として見ることで、求めることが可能です。
点Aを原点O(0,0)と設定します。
すると、求める直線AP3’は一次関数となります。
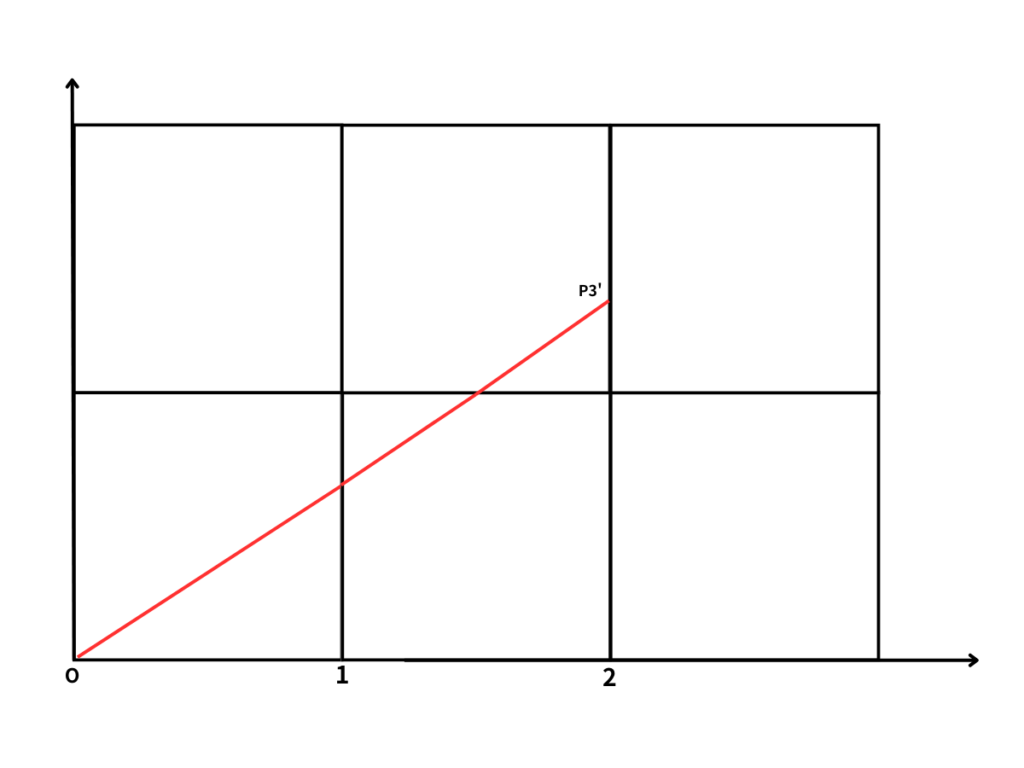
以下のように計算を進めて行きます。




このように幾何に見えて、実は関数の知識を活用して求める問題となります。
まとめ
というわけで、今回は幾何に見せて実は関数の問題を解説してみました。
角度を変えると実は別の問題だった。
これは何も数学だけでなく、実社会や日常においても同じことが言えますよね。
今回は容疑者Xの献身を題材に考えてみたのですが、石神はこんな複雑な問題を高校のテストにしていると考えたら、なんつー難易度の問題出してんだよ!とゾッとしますね笑
今回の内容で、何か気づきがあれば幸いです。